科目:gzsx
来源:2009-2010学年江西省重点学校高三联考数学试卷(文科)(解析版)
题型:解答题
已知椭圆

的离心率为

,右焦点为F(1,0),直线l经过点F且与椭圆交于A、B两点,O为坐标原点.
(1)求椭圆的方程;
(2)若P是椭圆上的一个动点,求|PO|
2+|PF|
2的最大值和最小值;
(3)当直线l绕点F转动时,试问:在x轴上是否存在定点S,使
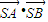
为常数,若存在,求出定点S的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:gzsx
来源:2009-2010学年浙江省温州中学高三(上)9月月考数学试卷(文科)(解析版)
题型:解答题
已知椭圆
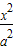
+
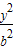
=1(a>b>0)的离心率为

,右焦点为F(1,0),直线l经过点F,且与椭圆交于A、B两点,O为坐标原点.
(I)求椭圆的标准方程;
(II)当直线l绕点F转动时,试问:在x轴上是否存在定点M,使得

为常数?若存在,求出定点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
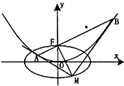
已知抛物线C:x
2=4y的焦点为F,过点F作直线l交抛物线C于A、B两点;椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率
e=.
(1)经过A、B两点分别作抛物线C的切线l
1,l
2,切线l
1与l
2相交于点M.证明:
•=•;
(2)椭圆E上是否存在一点M',经过点M'作抛物线C的两条切线M'A',M'B'(A',B'为切点),使得直线A'B'过点F?若存在,求出抛物线C与切线M'A',M'B'所围成图形的面积;若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知抛物线C:x
2=4y的焦点为F,过点F作直线l交抛物线C于A、B两点;椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率e=
.
(1)求椭圆E的方程;
(2)经过A、B两点分别作抛物线C的切线l
1、l
2,切线l
1与l
2相交于点M.证明:AB⊥MF;
(3)椭圆E上是否存在一点M′,经过点M′作抛物线C的两条切线M′A′、M′B(A′、B′为切点),使得直线A′B′过点F?若存在,求出抛物线C与切线M′A′、M′B所围成图形的面积;若不存在,试说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
 已知抛物线y2=4x的焦点为F,准线为l.
已知抛物线y2=4x的焦点为F,准线为l.
(1)求经过点F的直线l相切,且圆心在直线x-1=0上的圆的方程;
(2)设过点F且不与坐标轴垂直的直线交抛物线于A、B两点,线段AB的垂直平分线与x轴交于点M,求点M横坐标的取值范围.
查看答案和解析>>
科目:gzsx
来源:2012年福建省宁德市高三毕业班质量检查数学试卷(理科)(解析版)
题型:解答题
已知抛物线y
2=4x的焦点为F,准线为l.
(1)求经过点F的直线l相切,且圆心在直线x-1=0上的圆的方程;
(2)设过点F且不与坐标轴垂直的直线交抛物线于A、B两点,线段AB的垂直平分线与x轴交于点M,求点M横坐标的取值范围.
查看答案和解析>>
科目:gzsx
来源:2012年福建省宁德市高三毕业班质量检查数学试卷(文科)(解析版)
题型:解答题
已知抛物线y
2=4x的焦点为F,准线为l.
(1)求经过点F的直线l相切,且圆心在直线x-1=0上的圆的方程;
(2)设过点F且不与坐标轴垂直的直线交抛物线于A、B两点,线段AB的垂直平分线与x轴交于点M,求点M横坐标的取值范围.

查看答案和解析>>
科目:gzsx
来源:2010年吉林省长春市农安实验中学高考数学冲刺试卷(解析版)
题型:解答题
已知抛物线C:x
2=4y的焦点为F,过点F作直线l交抛物线C于A、B两点;椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率e=

.
(1)求椭圆E的方程;
(2)经过A、B两点分别作抛物线C的切线l
1、l
2,切线l
1与l
2相交于点M.证明:AB⊥MF;
(3)椭圆E上是否存在一点M′,经过点M′作抛物线C的两条切线M′A′、M′B(A′、B′为切点),使得直线A′B′过点F?若存在,求出抛物线C与切线M′A′、M′B所围成图形的面积;若不存在,试说明理由.
查看答案和解析>>
科目:gzsx
来源:2010年山东省高考数学押题卷(理科)(解析版)
题型:解答题
已知抛物线C:x
2=4y的焦点为F,过点F作直线l交抛物线C于A、B两点;椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率e=

.
(1)求椭圆E的方程;
(2)经过A、B两点分别作抛物线C的切线l
1、l
2,切线l
1与l
2相交于点M.证明:AB⊥MF;
(3)椭圆E上是否存在一点M′,经过点M′作抛物线C的两条切线M′A′、M′B(A′、B′为切点),使得直线A′B′过点F?若存在,求出抛物线C与切线M′A′、M′B所围成图形的面积;若不存在,试说明理由.
查看答案和解析>>
科目:gzsx
来源:2010年山东省高考数学押题试卷(理科)(解析版)
题型:解答题
已知抛物线C:x
2=4y的焦点为F,过点F作直线l交抛物线C于A、B两点;椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率e=

.
(1)求椭圆E的方程;
(2)经过A、B两点分别作抛物线C的切线l
1、l
2,切线l
1与l
2相交于点M.证明:AB⊥MF;
(3)椭圆E上是否存在一点M′,经过点M′作抛物线C的两条切线M′A′、M′B(A′、B′为切点),使得直线A′B′过点F?若存在,求出抛物线C与切线M′A′、M′B所围成图形的面积;若不存在,试说明理由.
查看答案和解析>>
科目:gzsx
来源:2011年江西省抚州市临川二中高考数学一模试卷(理科)(解析版)
题型:解答题
已知抛物线C:x
2=4y的焦点为F,过点F作直线l交抛物线C于A、B两点;椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率e=

.
(1)求椭圆E的方程;
(2)经过A、B两点分别作抛物线C的切线l
1、l
2,切线l
1与l
2相交于点M.证明:AB⊥MF;
(3)椭圆E上是否存在一点M′,经过点M′作抛物线C的两条切线M′A′、M′B(A′、B′为切点),使得直线A′B′过点F?若存在,求出抛物线C与切线M′A′、M′B所围成图形的面积;若不存在,试说明理由.
查看答案和解析>>
科目:gzsx
来源:2010年广东省深圳市高考数学二模试卷(理科)(解析版)
题型:解答题
已知抛物线C:x
2=4y的焦点为F,过点F作直线l交抛物线C于A、B两点;椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率e=

.
(1)求椭圆E的方程;
(2)经过A、B两点分别作抛物线C的切线l
1、l
2,切线l
1与l
2相交于点M.证明:AB⊥MF;
(3)椭圆E上是否存在一点M′,经过点M′作抛物线C的两条切线M′A′、M′B(A′、B′为切点),使得直线A′B′过点F?若存在,求出抛物线C与切线M′A′、M′B所围成图形的面积;若不存在,试说明理由.
查看答案和解析>>
科目:gzsx
来源:2010-2011学年北京市东城区东直门中学高考数学提高测试试卷6(理科)(解析版)
题型:解答题
已知抛物线C:x
2=4y的焦点为F,过点F作直线l交抛物线C于A、B两点;椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率e=

.
(1)求椭圆E的方程;
(2)经过A、B两点分别作抛物线C的切线l
1、l
2,切线l
1与l
2相交于点M.证明:AB⊥MF;
(3)椭圆E上是否存在一点M′,经过点M′作抛物线C的两条切线M′A′、M′B(A′、B′为切点),使得直线A′B′过点F?若存在,求出抛物线C与切线M′A′、M′B所围成图形的面积;若不存在,试说明理由.
查看答案和解析>>
科目:gzsx
来源:2011年河南省三市高三第二次调研数学试卷(理科)(解析版)
题型:解答题
已知抛物线C:x
2=4y的焦点为F,过点F作直线l交抛物线C于A、B两点;椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率

.
(1)经过A、B两点分别作抛物线C的切线l
1,l
2,切线l
1与l
2相交于点M.证明:

;
(2)椭圆E上是否存在一点M',经过点M'作抛物线C的两条切线M'A',M'B'(A',B'为切点),使得直线A'B'过点F?若存在,求出抛物线C与切线M'A',M'B'所围成图形的面积;若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知抛物线C:x
2=4y的焦点为F,过点F作直线l交抛物线C于A、B两点;椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率e=
.
(1)求椭圆E的方程;
(2)经过A、B两点分别作抛物线C的切线l
1、l
2,切线l
1与l
2相交于点M.证明:点M定在直线y=-1上;
(3)椭圆E上是否存在一点M′,经过点M′作抛物线C的两条切线M′A′、M′B′(A′、B′为切点),使得直线A′B′过点F?若存在,求出切线M′A′、M′B′的方程;若不存在,试说明理由.
查看答案和解析>>
科目:gzsx
来源:2016届安徽省高三上第五次月考文科数学试卷(解析版)
题型:选择题
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
1.
已知抛物线C:x
2=2py(p>0)的焦点为F(0,1),过点F作直线l交抛物线C于A,B两点.椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率$e=\frac{{\sqrt{3}}}{2}$.
(1)分别求抛物线C和椭圆E的方程;
(2)经过A,B两点分别作抛物线C的切线l
1,l
2,切线l
1与l
2相交于点M.证明:AB⊥MF;
(3)椭圆E上是否存在一点M′,经过点M′作抛物线C的两条切线M′A′,M′B′(A′,B′为切点),使得直线A′B′过点F?若存在,求出点M′及两切线方程,若不存在,试说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
11.

已知抛物线C:y
2=2px(p>0)的焦点为F,过F作垂直于x轴的直线交抛物线于A,B,两点,△AOB的面积为8,直线l与抛物线C相切于Q点,P是l上一点(不与Q重合).
(Ⅰ)求抛物线C的方程;
(Ⅱ)若以线段PQ为直径的圆恰好经过F,求|PF|的最小值.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
19.已知抛物线C:y2=2px(p>0)的焦点为F,直线y=4与f'(x)=0轴y的交点为R,与抛物线C的交点为O,且|QF|=$\frac{5}{4}$|RQ|.已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F1与抛物线C的焦点重合,且离心率为$\frac{1}{2}$
(Ⅰ)求抛物线C和椭圆E的标准方程;
(Ⅱ)若椭圆E的长轴的两端点为A,B,点P为椭圆上异于A,B的动点,定直线x=4与直线PA,PB分别交于M,N两点.请问以MN为直径的圆是否经过x轴上的定点,若存在,求出定点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
10.已知抛物线y2=-4x的焦点为F,准线为l
(1)求经过点F与直线l相切,且圆心在直线x+y-1=0上的圆的方程;
(2)设过点F且不与坐标轴垂直的直线交抛物线于A,B两点,线段AB的垂直平分线与x轴交于点M,求点M横坐标的取值范围.
查看答案和解析>>

 的离心率为
的离心率为 ,右焦点为F(1,0),直线l经过点F且与椭圆交于A、B两点,O为坐标原点.
,右焦点为F(1,0),直线l经过点F且与椭圆交于A、B两点,O为坐标原点.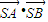 为常数,若存在,求出定点S的坐标;若不存在,请说明理由.
为常数,若存在,求出定点S的坐标;若不存在,请说明理由.
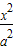 +
+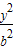 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,右焦点为F(1,0),直线l经过点F,且与椭圆交于A、B两点,O为坐标原点.
,右焦点为F(1,0),直线l经过点F,且与椭圆交于A、B两点,O为坐标原点. 为常数?若存在,求出定点M的坐标;若不存在,请说明理由.
为常数?若存在,求出定点M的坐标;若不存在,请说明理由. 已知抛物线C:x2=4y的焦点为F,过点F作直线l交抛物线C于A、B两点;椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率e=
已知抛物线C:x2=4y的焦点为F,过点F作直线l交抛物线C于A、B两点;椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率e= 已知抛物线y2=4x的焦点为F,准线为l.
已知抛物线y2=4x的焦点为F,准线为l.

 .
. .
. .
. .
. .
. .
. .
. ;
;
 的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在y轴上,则
的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在y轴上,则 与
与 的面积之比是( )
的面积之比是( )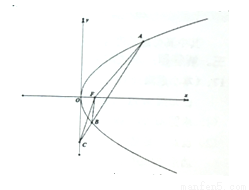
 B.
B. C.
C. D.
D.
 已知抛物线C:x2=2py(p>0)的焦点为F(0,1),过点F作直线l交抛物线C于A,B两点.椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率$e=\frac{{\sqrt{3}}}{2}$.
已知抛物线C:x2=2py(p>0)的焦点为F(0,1),过点F作直线l交抛物线C于A,B两点.椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率$e=\frac{{\sqrt{3}}}{2}$. 已知抛物线C:y2=2px(p>0)的焦点为F,过F作垂直于x轴的直线交抛物线于A,B,两点,△AOB的面积为8,直线l与抛物线C相切于Q点,P是l上一点(不与Q重合).
已知抛物线C:y2=2px(p>0)的焦点为F,过F作垂直于x轴的直线交抛物线于A,B,两点,△AOB的面积为8,直线l与抛物线C相切于Q点,P是l上一点(不与Q重合).