练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >在△abc中.ab=√2,bc=1

    在△abc中.ab=√2,bc=1答案解析

    科目：gzsx 来源： 题型：

    如图,在△ABC中,AC=2,BC=1,cosC=.

    (1)求AB的值;

    (2)求sin(2A+C)的值.

    查看答案和解析>>

    科目：czsx 来源：2013-2014学年福建省九年级上学期期末考试数学试卷（A）（解析版） 题型：解答题

    在△ABC中,AB＝BC＝2,∠ABC＝120°,将△ABC绕点B顺时针旋转角(0°＜α＜90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC,BC于D,F两点．(12分)

                     图(a)                                      图(b)

    (1)如图(a),观察并猜想,在旋转过程中,线段EA1与FC是怎样的数量关系?并证明你的结论;

    (2)如图(b),当α＝30°时,试判断四边形BC1DA的形状,并说明理由;

    (3)在(2)的情况下,求ED的长．

     

    查看答案和解析>>

    科目：czsx 来源：不详 题型：解答题

    在△ABC中,AB＝BC＝2,∠ABC＝120°,将△ABC绕点B顺时针旋转角(0°＜α＜90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC,BC于D,F两点．(12分)

    图(a)                                     图(b)
    (1)如图(a),观察并猜想,在旋转过程中,线段EA1与FC是怎样的数量关系?并证明你的结论;
    (2)如图(b),当α＝30°时,试判断四边形BC1DA的形状,并说明理由;
    (3)在(2)的情况下,求ED的长．

    查看答案和解析>>

    科目：czsx 来源： 题型：


    在△ABC中,AB=2,BC=1,∠ABC=45°,以AB为一边作等腰直角三角形ABD,使∠ABD=90°,连接CD,则线段CD的长为　　　　.

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如图,在△ABC中,AB=2,BC=3.6, ∠B=600,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为______.

    查看答案和解析>>

    科目：czsx 来源：2016届辽宁省大石桥市九年级上第三次测试数学试卷（解析版） 题型：填空题

    如图,在△ABC中,AB=2 BC=3．6, ∠B=600,将△ABC绕点A按顺时针旋转一定角度得到

    △ADE,当点B的对应点D恰好落在BC边上时,则CD的长为_____．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    如图，在△ABC中，AC=BC=1，∠ACB=90°，点D在斜边AB上，∠BCD=α（0＜α＜
    π2
    ）．把△BCD沿CD折起到△B′CD的位置，使平面B′CD⊥平面ACD．
    （1）求点B′到平面ACD的距离（用α表示）；
    （2）当AD⊥B′C时，求三棱锥B′-ACD的体积．

    查看答案和解析>>

    科目：czsx 来源：数学教研室 题型：044

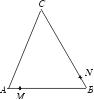
    如图所示,在△ABC中,AB=30cm,BC=35cm,∠B=60°,有一动点M自A向B以1cm/s的速度运动,动点N自B向C以2cm/s的速度运动.若M、N同时分别从A、B出发.

    (1)请你推算一下出发几秒后,△BMN为等边三角形?

    (2)出发几秒后,△BMN为直角三角形?通过推算你有什么结论?

     

    查看答案和解析>>

    科目：gzsx 来源： 题型：解答题

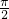    如图，在△ABC中，AC=BC=1，∠ACB=90°，点D在斜边AB上，∠BCD=α（0＜α＜数学公式）．把△BCD沿CD折起到△B′CD的位置，使平面B′CD⊥平面ACD．
    （1）求点B′到平面ACD的距离（用α表示）；
    （2）当AD⊥B′C时，求三棱锥B′-ACD的体积．

    查看答案和解析>>

    科目：gzsx 来源：2011年广东省广州市仲元中学高三数学专题训练：直线、平面、简单几何（解析版） 题型：解答题

    如图，在△ABC中，AC=BC=1，∠ACB=90°，点D在斜边AB上，∠BCD=α（0＜α＜）．把△BCD沿CD折起到△B′CD的位置，使平面B′CD⊥平面ACD．
    （1）求点B′到平面ACD的距离（用α表示）；
    （2）当AD⊥B′C时，求三棱锥B′-ACD的体积．

    查看答案和解析>>

    科目：gzsx 来源： 题型：解答题

    18．如图（1），在△ABC中，AC=BC=1，∠ACB=90°，D是AB边上一点，沿CD将图形折叠成图（2），使得二面角B-CD-A是直二面角．

    （1）若D是AB边的中点，求二面角C-AB-D的大小；
    （2）若AD=2BD，求点B到平面ACD的距离；
    （3）是否存在一点D，使得二面角C-AB-D是直二面角？若存在，求$\frac{BD}{AD}$的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：解答题

    如图,A,B,C,D为空间四点.在△ABC中,AB=2,AC=BC=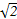.等边三角形ADB以AB为轴转动.

    (1)当平面ADB⊥平面ABC时,求CD.
    (2)当△ADB转动时,是否总有AB⊥CD?证明你的结论.

    查看答案和解析>>

    科目：gzsx 来源：不详 题型：解答题

    如图,A,B,C,D为空间四点.在△ABC中,AB=2,AC=BC=.等边三角形ADB以AB为轴转动.

    (1)当平面ADB⊥平面ABC时,求CD.
    (2)当△ADB转动时,是否总有AB⊥CD?证明你的结论.

    查看答案和解析>>

    科目：gzsx 来源：2014年高考数学全程总复习课时提升作业四十六第七章第五节练习卷（解析版） 题型：解答题

    如图,A,B,C,D为空间四点.在△ABC中,AB=2,AC=BC=.等边三角形ADB以AB为轴转动.

    (1)当平面ADB⊥平面ABC时,求CD.

    (2)当△ADB转动时,是否总有AB⊥CD?证明你的结论.

     

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2005•海淀区二模）如图所示，在△ABC中，AC=BC=1，∠ACB=90°，点D在斜边AB上，∠BCD=α（0＜α＜
    π2
    ）．把△ABC沿CD折起到△B′CD的位置，使平面B′CD⊥平面ACD
    （Ⅰ）求点B′到平面ACD的距离（用α表示）；
    （Ⅱ）当AD⊥B′C时，求三棱锥B′-ACD的体积；
    （Ⅲ）当点B′在平面ACD内的射影为线段CD的中点时，求异面直线AD与B′C所成角的大小．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2005•海淀区二模）如图所示，在△ABC中，AC=BC=1，∠ACB=90°，点D在斜边AB上，∠BCD=α(0＜α＜
    π
    2
    )    ．把△ABC沿CD折起到△B′CD的位置，使平面B′CD⊥平面ACD
    （Ⅰ）求点Bn到平面ACD的距离（用α表示）；
    （Ⅱ）当AD⊥BnC时，求三棱锥Bn-ACD的体积；
    （Ⅲ）当α=
    π
    3
    时，求二面角Bn-AC-D的正切值．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    在△ABC中AB=BC，∠ABC=20°，在AB边上取一点M，使BM=AC．求∠AMC的度数．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    精英家教网在△ABC中AB=AC=5，BC=6，D为BC中点，DE⊥AC，则DE的长为（　　）
    A、
    6
    5
    B、
    9
    5
    C、
    12
    5
    D、
    16
    5

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    在△ABC中AB=c，AC=b，D为线段BC上一点，且∠BAD=α，∠CAD=β，线段AD=l．
    （1）求证：
    sinα
    b
    +
    sinβ
    c
    =
    sin(α+β)
    l

    （2）若AB=4
    		2
    ，AC=4    ，∠BAD=30°，∠CAD=45°，试求线段AD的长．

    查看答案和解析>>

    科目：czsx 来源：数学教研室 题型：022

    在△ABC中AB=13，BC=10，AD⊥BC于D且AD=12，则AC=_______．

    查看答案和解析>>