已知抛物线y=二分之一x2-二分之三x-2与x轴答案解析
科目:czsx
来源:2015年初中毕业升学考试(湖南益阳卷)数学(解析版)
题型:解答题
(15分)(2015•益阳)已知抛物线E1:y=x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A、B关于y 轴的对称点分别为点A′,B′.
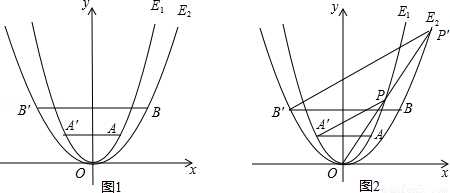
(1)求m的值及抛物线E2所表示的二次函数的表达式;
(2)如图1,在第一象限内,抛物线E1上是否存在点Q,使得以点Q、B、B′为顶点的三角形为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由;
(3)如图2,P为第一象限内的抛物线E1上与点A不重合的一点,连接OP并延长与抛物线E2相交于点P′,求△PAA′与△P′BB′的面积之比.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
4.已知抛物线C
1:y=-$\frac{1}{2}$x
2+mx+m+$\frac{1}{2}$.
(1)①无论m取何值,抛物线经过定点P(-1,0);
②随着m的取值变化,顶点M(x,y)随之变化,y是x的函数,则其函数C
2关系式为y=$\frac{1}{2}{x}^{2}+x+\frac{1}{2}$;
(2)如图1,若该抛物线C
1与x轴仅有一个公共点,请在图1中画出顶点M满足的函数C
2的大致图象,平行于y轴的直线l分别交C
1、C
2于点A、B,若△PAB为等腰直角三角形,判断直线l满足的条件,并说明理由;
(3)如图2,抛物线C
1的顶点M在第二象限,交x轴于另一点C,抛物线上点M与点P之间一点D的横坐标为-2,连接PD、CD、CM、DM,若S
△PCD=S
△MCD,求二次函数的解析式.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
19.已知抛物线E
1:y=x
2经过点A(1,m),以原点为顶点的抛物线E
2经过点B(2,2),点A、B关于y 轴的对称点分别为点A′,B′.
(1)求m的值及抛物线E
2所表示的二次函数的表达式;
(2)如图1,在第一象限内,抛物线E
1上是否存在点Q,使得以点Q、B、B′为顶点的三角形为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由;
(3)如图2,P为第一象限内的抛物线E
1上与点A不重合的一点,连接OP并延长与抛物线E
2相交于点P′,求△PAA′与△P′BB′的面积之比.
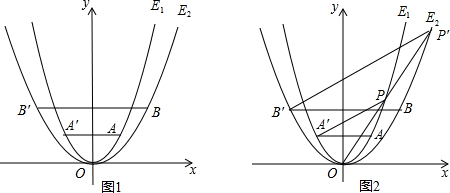
查看答案和解析>>
科目:czsx
来源:
题型:解答题
6.

已知,抛物线C
1:y=-$\frac{1}{2}$x
2+mx+m+$\frac{1}{2}$.
(1)①无论m取何值,抛物线经过定点P(-1,0);
②随着m的取值的变化,顶点M(x,y)随之变化,y是x的函数,则函数C
2的关系式为:y=$\frac{1}{2}$(x+1)
2;
(2)如图1,抛物线C
1与x轴仅有一个公共点,请在图1画出顶点M满足的函数C
2的大致图象,平行于y轴的直线l分别交C
1、C
2于点A、B,若△PAB为等腰直角三角形,判断直线l满足的条件,并说明理由;
(3)如图2,二次函数的图象C
1的顶点M在第二象限、交x轴于另一点C,抛物线上点M与点P之间一点D的横坐标
为-2,连接PD、CD、CM、DM,若S
△PCD=S
△MCD,求二次函数的解析式.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
5.
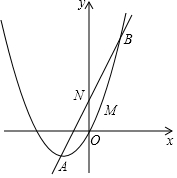
已知二次函数y=x
2+2x+$\frac{k-1}{2}$与x轴有两个交点,且k为正整数.
(1)求k的值;
(2)当二次函数y=x
2+2x+$\frac{k-1}{2}$图象经过原点时,直线y=3x+2与之交于A、B两点,若M是抛物线上在直线y=3x+2下方的一个动点,△MAB面积是否存在最大值?若存在,请求出M点坐标,并求出△MAB面积最大值;若不存在,请说明理由.
(3)将(2)中的二次函数图象x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分保持不变,翻折后的图象与原图象x轴上方的部分组成一个新图象.若直线y=kx+2(k>0)与该新图象恰好有三个公共点,求k的值.
查看答案和解析>>
科目:czsx
来源:
题型:
如图①,在平面直角坐标系中,一块等腰直角三角板ABC的直角顶点A在y轴上,坐标为(0,-1),另一顶点B坐标为(-2,0),已知二次函数y=
x
2+bx+c的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A′D′∥y轴且经过点B,直尺沿x轴正方向平移,当A′D′与y轴重合时运动停止.
(1)求点C的坐标及二次函数的关系式;
(2)若运动过程中直尺的边A′D′交边BC于点M,交抛物线于点N,求线段MN长度的最大值;
(3)如图②,设点P为直尺的边A′D′上的任一点,连接PA、PB、PC,Q为BC的中点,试探究:在直尺平移的过程中,当PQ=
时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.
(说明:点与抛物线的位置关系可分为三类,例如,图②中,点A在抛物线内,点C在抛物线上,点D′在抛物线外.)
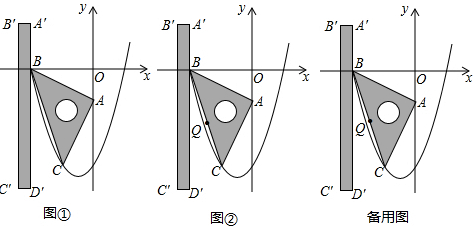
查看答案和解析>>
科目:czsx
来源:2014-2015学年江苏省苏州市九年级上学期期末考试数学试卷(解析版)
题型:解答题
如图①,在平面直角坐标系中,一块等腰直角三角板ABC的直角顶点A在y轴上,坐标为(0,-1),另一顶点B坐标为(-2,0),已知二次函数y= x2+bx+c的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A'D'∥y轴且经过点B,直尺沿x轴正方向平移,当A'D'与y轴重合时运动停止.
x2+bx+c的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A'D'∥y轴且经过点B,直尺沿x轴正方向平移,当A'D'与y轴重合时运动停止.
(1)求点C的坐标及二次函数的关系式;
(2)若运动过程中直尺的边A'D'交边BC于点M,交抛物线于点N,求线段MN长度的最大值;
(3)如图②,设点P为直尺的边A'D'上的任一点,连接PA、PB、PC,Q为BC的中点,试探究:在直尺平移的过程中,当PQ=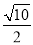 时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.
时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.
(说明:点与抛物线的位置关系可分为三类,例如,图②中,点A在抛物线内,点C在抛物线上,点D'在抛物线外.)

查看答案和解析>>
科目:czsx
来源:
题型:
如图①,在平面直角坐标系中,一块等腰直角三角板ABC的直角顶点A在y轴上,坐标为(0,﹣1),另一顶点B坐标为(﹣2,0),已知二次函数y= x2+bx+c的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A′D′∥y轴且经过点B,直尺沿x轴正方向平移,当A′D′与y轴重合时运动停止.
x2+bx+c的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A′D′∥y轴且经过点B,直尺沿x轴正方向平移,当A′D′与y轴重合时运动停止.
(1)求点C的坐标及二次函数的关系式;
(2)若运动过程中直尺的边A′D′交边BC于点M,交抛物线于点N,求线段MN长度的最大值;
(3)如图②,设点P为直尺的边A′D′上的任一点,连接PA、PB、PC,Q为BC的中点,试探究:在直尺平移的过程中,当PQ=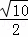 时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.
时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.
(说明:点与抛物线的位置关系可分为三类,例如,图②中,点A在抛物线内,点C在抛物线上,点D′在抛物线外.)



查看答案和解析>>




 已知,抛物线C1:y=-$\frac{1}{2}$x2+mx+m+$\frac{1}{2}$.
已知,抛物线C1:y=-$\frac{1}{2}$x2+mx+m+$\frac{1}{2}$. 已知二次函数y=x2+2x+$\frac{k-1}{2}$与x轴有两个交点,且k为正整数.
已知二次函数y=x2+2x+$\frac{k-1}{2}$与x轴有两个交点,且k为正整数.
 x2+bx+c的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A'D'∥y轴且经过点B,直尺沿x轴正方向平移,当A'D'与y轴重合时运动停止.
x2+bx+c的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A'D'∥y轴且经过点B,直尺沿x轴正方向平移,当A'D'与y轴重合时运动停止.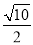 时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.
时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.
 x2+bx+c的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A′D′∥y轴且经过点B,直尺沿x轴正方向平移,当A′D′与y轴重合时运动停止.
x2+bx+c的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A′D′∥y轴且经过点B,直尺沿x轴正方向平移,当A′D′与y轴重合时运动停止.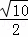 时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.
时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.

