精英家教网 >
试题搜索列表 >定义在R上的函数f(x)满足f(x+y)=f(x)+f(y)+2xy,则f(0)
定义在R上的函数f(x)满足f(x+y)=f(x)+f(y)+2xy,则f(0)答案解析
科目:czsx
来源:
题型:
(本题满分16分) 本题共有2个小题,第1小题满分10分,第2小题满分6分.
定义在R上的奇函数

有最小正周期4,且
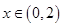
时,

(1)判断并证明

在

上的单调性,并求

在
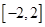
上的解析式;
(2)当
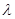
为何值时,关于
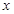
的方程

在

上有实数解?
查看答案和解析>>
科目:czsx
来源:
题型:
(2012•石家庄二模)如图1,在一次航海模型船训练中,A
1B
1和A
2B
2是水面上相邻的两条赛道(看成两条互相平行的线段).甲船在赛道A
1B
1上从A
1处出发,到达B
1后,以同样的速度返回A
1处,然后重复上述过程;乙船在赛道A
2B
2上以2m/s的速度从B
2处出发,到达A
2后以相同的速度回到B
2处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两船同时出发,设离开池边B
1B
2的距离为y(m),运动时间为t(s),甲船运动时,y(m)与t(s)的函数图象如图2所示.

(1)赛道的长度是
90
90
m,甲船的速度是
3
3
m/s;
(2)分别求出甲船在0≤t≤30和30<t≤60时,y关于t的函数关系式;
(3)求出乙船由B
2到达A
2的时间,并在图2中画出乙船在3 分钟内的函数图象;
(4)请你根据(3)中所画的图象直接判断,若从甲、乙两船同时开始出发到3分钟为止,甲、乙共相遇了几次?
查看答案和解析>>
科目:czsx
来源:
题型:
(2012•黄石)已知抛物线C
1的函数解析式为y=ax
2+bx-3a(b<0),若抛物线C
1经过点(0,-3),方程ax
2+bx-3a=0的两根为x
1,x
2,且|x
1-x
2|=4.
(1)求抛物线C
1的顶点坐标.
(2)已知实数x>0,请证明x+
≥2,并说明x为何值时才会有x+
=2.
(3)若将抛物线先向上平移4个单位,再向左平移1个单位后得到抛物线C
2,设A(m,y
1),B(n,y
2)是C
2上的两个不同点,且满足:∠AOB=90°,m>0,n<0.请你用含m的表达式表示出△AOB的面积S,并求出S的最小值及S取最小值时一次函数OA的函数解析式.
(参考公式:在平面直角坐标系中,若P(x
1,y
1),Q(x
2,y
2),则P,Q两点间的距离为
)
查看答案和解析>>
科目:czsx
来源:
题型:
如图,一次函数
y=-x+的函数图象与x轴、y轴分别交于点A、B,以线段AB为
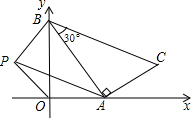
直角边在第一象限内作Rt△ABC,且使∠ABC=30°.
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,
),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值;
(3)是否存在使△QAB是等腰三角形并且在坐标轴上的点Q?若存在,请写出点Q所有可能的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
按要求填空,并作图.
(1)请用描点法在直角坐标系上画出
y=的函数图象.
(2)点(12,
)在
y=的函数图象上吗?为什么?
查看答案和解析>>
科目:czsx
来源:
题型:
27、(任选一题,若两题都选按得分最少的题记分)
(1)甲乙两辆汽车在一条公路上匀速行驶,为了确定汽车的位置,我们用数轴Ox表示这条公路,原点O为零千米路标(如图1),并作如下约定:
①速度v>0,表示汽车向数轴正方向行驶;速度v<0,表示汽车向数轴负方向行驶;速度v=0,表示汽车静止.
②汽车位置在数轴上的坐标s>0,表示汽车位于零千米路标的右侧;汽车位置在数轴上的坐标s<0,表示汽车位于零千米路标的左侧;汽车位置在数轴上的坐标s=0,表示汽车恰好位于零千米路标处.
遵照上述约定,将这两辆汽车在公路上匀速行驶的情况,以一次函数图象的形式画在了同一直角坐标系中,如图2,请解答下列问题:
①就这两个一次函数图象所反映的两汽车在这条公路上行驶的状况填写如下的表格.

②甲乙两车能否相遇?如能相遇,求相遇时的时刻及在公路上的位置;如不能相遇,请说明理由.

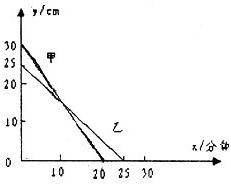
(2)在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余的高度y(cm)与燃烧时间x(分钟)的关系如下图所示,根据图象提供的信息解答下列问题:
①指出两根蜡烛燃烧前的高度;
②分别求出甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
③x为何值时,甲、乙两根蜡烛在燃烧过程中的高度相等.
查看答案和解析>>
科目:czsx
来源:
题型:
在锐角三角形纸片ABC中,BC=4,高AD=3,直线EF∥BC,分别交线段AB,AC,AD于E,F,G,设EF=x.
(1)求线段AG的长(用含x的代数式表示);
(2)将纸片沿直线EF折叠,设点A落在平面上的点为P,△PEF与四边形BCFE重叠部分的面积为y,求y关于x的函数关系式,并写出x的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:
下列四个函数中,图象的顶点在y轴上的函数是( )
| A、y=x2-3x+2 | B、y=5-x2 | C、y=-x2+2x | D、y=x2-4x+4 |
查看答案和解析>>
科目:czsx
来源:
题型:
如图,将边长为4的正方形纸片,置于平面直角坐标系内,顶点A在坐标原点,点B在x轴的正半轴上,E、F分
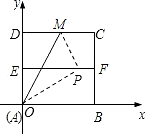
别是AD、BC的中点,点M在DC上.将△ADM沿AM折叠,点D折叠后恰好落在EF上的点P处.
(1)求∠EAP的度数;
(2)求折痕AM所在直线的函数关系式;
(3)设H为直线AM上的点,是否存在这样的点H,使得以H、A、P为顶点的三角形是等腰三角形?若存在,请直接写出点H的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
(2007•海淀区二模)在平面直角坐标系xOy中,已知直线y=-
x+
交x轴于点C,交y轴于点A.等腰直角三角板OBD的顶点D与点C重合,如图A所示.把三角板绕着点O顺时针旋转,旋转角度为α(0°<α<180°),使B点恰好落在AC上的B'处,如图B所示.
(1)求图A中的点B的坐标;
(2)求α的值;
(3)若二次函数y=mx
2+3x的图象经过(1)中的点B,判断点B′是否在这条抛物线上,并说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:
(2012•黄陂区模拟)某超市开辟一个精品蔬菜柜,其中每天从菜农手中购进一种新鲜蔬菜200千克,其进货成本(含运输费)是每千克1元,根据超市规定,这种蔬菜只能当天销售,并且每千克的销售价不能超过8元,一天内没有销售完的蔬菜只能报废,而且这种新鲜蔬菜每天的损耗率是10%,根据市场调查这种蔬菜每天在

市场上的销售量y(单位:千克y≥0)与每千克的销售价x(元)之间的函数关系如图所示:
(1)求出每天销售量y与每千克销售价之间的函数关系式;
(2)根据题中的信息分析,每天销售利润最少是多少元?最多是多少元?
(3)当每千克销售价为多少元时,每天的销售利润不低于640元?
查看答案和解析>>
科目:czsx
来源:
题型:
如图,直线l:y=
x+
与x轴、y轴分别交于点B、C,以点A(1,0)为圆心,以AB的长为半径作⊙A,分别交x轴、y轴正半轴于点D、E,直线l与⊙A交于点F,分别过点B、F作⊙A的切线交于点M.
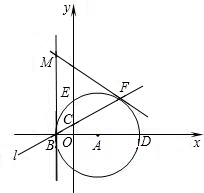
(1)直接写出点B、C的坐标;
(2)求直线MF的解析式;
(3)若点P是
上任意一点(不与B、F重合).连接BP、FP.过点M作MN∥PF,交直线l于点N.设PB=a,MN=b,求b与a的函数关系式,并写出自变量a的取值范围;
(4)若将(3)中的条件点P是
上任意一点,改为点P是⊙A上任意一点,其它条件不变.当点P在⊙A上的什么位置时,△BMN为直角三角形,并写出此时点N的坐标.(第(4)问直接写出结果,不要求证明或计算过程)
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在平面直角坐标系中,直线y=-2x+2与x轴、y轴分别相交于点A,B,四边形ABCD是正方形,反比例函数y=
在第一象限的图象经过点D.
(1)求D点的坐标,以及反比例函数的解析式;
(2)若K是双曲线上第一象限内的任意点,连接AK、BK,设四边形AOBK的面积为S;试推断当S达到最大值或最小值时,相应的K点横坐标;并直接写出S的取值范围.
(3)试探究:将正方形ABCD沿左右(或上下)一次平移若干个单位后,点C的对应点恰好落在双曲线上的方法.
查看答案和解析>>
科目:czsx
来源:
题型:
某课题学习小组在一次活动中对三角形的内接正方形的有关问题进行了探讨:
定义:如果一个正方形的四个顶点都在一个三角形的边上,那么我们就把这个正方形叫做三角形的内接正方形.
结论:在探讨过程中,有三位同学得出如下结果:
甲同学:在钝角、直角、不等边锐角三角形中分别存在
1
1
个、
2
2
个、
3
3
个大小不同的内接正方形.
乙同学:在直角三角形中,两个顶点都在斜边上的内接正方形的面积较大.
任务:(1)填充甲同学结论中的数据;
(2)乙同学的结果正确吗?若不正确,请举出一个反例并通过计算给予说明,若正确,请给出证明.
查看答案和解析>>
科目:czsx
来源:
题型:
(2013•黄埔区一模)若实数a、b在数轴上的位置如图所示,A(1,y
1)、B(2,y
2)是函数y=ax+b图象上的两点,则( )
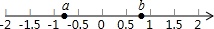
查看答案和解析>>

 有最小正周期4,且
有最小正周期4,且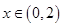 时,
时,
 在
在 上的单调性,并求
上的单调性,并求 在
在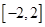 上的解析式;
上的解析式;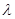 为何值时,关于
为何值时,关于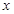 的方程
的方程 在
在 上有实数解?
上有实数解? 
 直角边在第一象限内作Rt△ABC,且使∠ABC=30°.
直角边在第一象限内作Rt△ABC,且使∠ABC=30°. 按要求填空,并作图.
按要求填空,并作图.


 别是AD、BC的中点,点M在DC上.将△ADM沿AM折叠,点D折叠后恰好落在EF上的点P处.
别是AD、BC的中点,点M在DC上.将△ADM沿AM折叠,点D折叠后恰好落在EF上的点P处.
 市场上的销售量y(单位:千克y≥0)与每千克的销售价x(元)之间的函数关系如图所示:
市场上的销售量y(单位:千克y≥0)与每千克的销售价x(元)之间的函数关系如图所示: (1)直接写出点B、C的坐标;
(1)直接写出点B、C的坐标;

 如图,在平面直角坐标系中,直线y=-2x+2与x轴、y轴分别相交于点A,B,四边形ABCD是正方形,反比例函数y=
如图,在平面直角坐标系中,直线y=-2x+2与x轴、y轴分别相交于点A,B,四边形ABCD是正方形,反比例函数y=