科目:gzsx
来源:
题型:
有下列四个命题:
(1)一定存在直线l,使函数
f(x)=lgx+lg的图象与函数g(x)=lg(-x)+2的图象关于直线l对称;
(2)在复数范围内,a+bi=0⇔a=0,b=0
(3)已知数列a
n的前n项和为S
n=1-(-1)
n,n∈N
*,则数列a
n一定是等比数列;
(4)过抛物线y
2=2px(p>0)上的任意一点M(x
°,y
°)的切线方程一定可以表示为y
0y=p(x+x
0).
则正确命题的序号为
.
查看答案和解析>>
科目:gzsx
来源:2009-2010学年上海市十校高三(上)第一次联考数学试卷(理科)(解析版)
题型:填空题
有下列四个命题:
(1)一定存在直线l,使函数

的图象与函数g(x)=lg(-x)+2的图象关于直线l对称;
(2)在复数范围内,a+bi=0⇔a=0,b=0
(3)已知数列a
n的前n项和为S
n=1-(-1)
n,n∈N
*,则数列a
n一定是等比数列;
(4)过抛物线y
2=2px(p>0)上的任意一点M(x
°,y
°)的切线方程一定可以表示为y
y=p(x+x
).
则正确命题的序号为
.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
有下列四个命题:
(1)一定存在直线l,使函数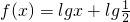 的图象与函数g(x)=lg(-x)+2的图象关于直线l对称;
的图象与函数g(x)=lg(-x)+2的图象关于直线l对称;
(2)在复数范围内,a+bi=0⇔a=0,b=0
(3)已知数列an的前n项和为Sn=1-(-1)n,n∈N*,则数列an一定是等比数列;
(4)过抛物线y2=2px(p>0)上的任意一点M(x°,y°)的切线方程一定可以表示为y0y=p(x+x0).
则正确命题的序号为________.
查看答案和解析>>
科目:gzsx
来源:2010-2011学年江苏省南通市四星高中四校高三联考数学试卷(解析版)
题型:解答题
有下列四个命题:
(1)一定存在直线l,使函数

的图象与函数g(x)=lg(-x)+2的图象关于直线l对称;
(2)在复数范围内,a+bi=0⇔a=0,b=0
(3)已知数列a
n的前n项和为S
n=1-(-1)
n,n∈N
*,则数列a
n一定是等比数列;
(4)过抛物线y
2=2px(p>0)上的任意一点M(x
°,y
°)的切线方程一定可以表示为y
y=p(x+x
).
则正确命题的序号为
.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知数列an的前n项和为Sn.
(Ⅰ)若数列an是等比数列,满足2a1+a3=3a2,a3+2是a2,a4的等差中项,求数列an的通项公式;
(Ⅱ)是否存在等差数列ann∈N*,使对任意n∈N*都有an•Sn=2n2(n+1)?若存在,请求出所有满足条件的等差数列;若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知数列an的前n项和为Sn,且a1=1,Sn=n2an(n∈N),
(1)试计算S1,S2,S3,S4,并猜想Sn的表达式;
(2)证明你的猜想,并求出an的表达式.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知数列a
n的前n项和为S
n=2n
2-3n+1,则它的通项公式a
n=
.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知数列an}的前n项和为sn,满足(p-1)sn=p2-an,其中p为正常数,且p≠1.
(1)求证:数列{an}为等比数列,并求出{an}的通项公式;
(2)若存在正整数M,使得当n≥M时,a1a4a7…a3n-2>a36恒成立,求出M的最小值;
(3)当p=2时,数列an,2xan+1,2yan+2成等差数列,其中x,y均为整数,求出x,y的值.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知数列a
n的前n项和为S
n,a
1=1,na
n=S
n+2n(n-1)(n∈N
*).
(I)求数列a
n的通项公式;
(II)设
Tn=++…+,求T
n的值.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知数列a
n的前n项和为S
n,对任意n∈N*,点(n,S
n)都在函数f(x)=2x
2-x的图象上.
(1)求数列a
n的通项公式;
(2)设
bn=,且数列b
n是等差数列,求非零常数p的值;
(3)设
cn=,T
n是数列c
n的前n项和,求使得
Tn<对所有n∈N*都成立的最小正整数m.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知数列a
n的前n项和为S
n,a
1=1,S
n=a
n+1-3n-1,n∈N
*.
(Ⅰ)证明:数列a
n+3是等比数列;
(Ⅱ)对k∈N
*,设
f(n)= | | Sn-an+3n n=2k-1 | | log2(an+3) n=2k. |
| |
求使不等式cos(mπ)[f(2m
2)-f(m)]≤0成立的正整数m的取值范围..
查看答案和解析>>
科目:gzsx
来源:
题型:
已知数列a
n的前n项和为S
n,a
1=2,na
n+1=S
n+n(n+1),
(1)求数列a
n的通项公式;
(2)设
bn=,如果对一切正整数n都有b
n≤t,求t的最小值.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知数列
的前n项和为S
n,且S
n=1-a
n (n∈N
*)
(I )求数列
的通项公式;
(Ⅱ)已知数列
的通项公式b
n=2n-1,记c
n=a
nb
n,求数列
的前n项和T
n.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知数列a
n的前n项和为S
n,点(n,S
n)(n∈N
*)在函数f(x)=3x
2-2x的图象上,
(1)求数列a
n的通项公式;
(2)设
bn=,求数列b
n的前n项和T
n.
查看答案和解析>>
科目:gzsx
来源:2011-2012学年山东省泰安市新泰市新汶中学高二(上)期末数学模拟试卷(理科)(解析版)
题型:解答题
已知数列a
n的前n项和为S
n,a
1=1,na
n=S
n+2n(n-1)(n∈N
*).
(I)求数列a
n的通项公式;
(II)设

,求T
n的值.
查看答案和解析>>
科目:gzsx
来源:2010-2011学年湖北省武汉市武昌区高二(上)期末数学试卷(文科)(解析版)
题型:填空题
已知数列an的前n项和为Sn=2n2-3n+1,则它的通项公式an= .
查看答案和解析>>
科目:gzsx
来源:2010年山东省鲁实中学高考数学二模试卷(文科)(解析版)
题型:解答题
已知数列a
n的前n项和为S
n,点(n,S
n)(n∈N
*)在函数f(x)=3x
2-2x的图象上,
(1)求数列a
n的通项公式;
(2)设

,求数列b
n的前n项和T
n.
查看答案和解析>>
科目:gzsx
来源:2009-2010学年北京市顺义区牛栏山一中高三(上)12月月考数学试卷(理科)(解析版)
题型:填空题
已知数列an的前n项和为Sn=2n2-3n+1,则它的通项公式an= .
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
已知数列an的前n项和为Sn,且a1=1,Sn=n2an(n∈N),
(1)试计算S1,S2,S3,S4,并猜想Sn的表达式;
(2)证明你的猜想,并求出an的表达式.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年山东省德州市夏津一中高三(上)期末数学模拟试卷(理科)(解析版)
题型:解答题
已知数列an的前n项和为Sn,且a1=1,Sn=n2an(n∈N),
(1)试计算S1,S2,S3,S4,并猜想Sn的表达式;
(2)证明你的猜想,并求出an的表达式.
查看答案和解析>>

 的图象与函数g(x)=lg(-x)+2的图象关于直线l对称;
的图象与函数g(x)=lg(-x)+2的图象关于直线l对称;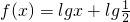 的图象与函数g(x)=lg(-x)+2的图象关于直线l对称;
的图象与函数g(x)=lg(-x)+2的图象关于直线l对称; 的图象与函数g(x)=lg(-x)+2的图象关于直线l对称;
的图象与函数g(x)=lg(-x)+2的图象关于直线l对称; ,求Tn的值.
,求Tn的值. ,求数列bn的前n项和Tn.
,求数列bn的前n项和Tn.