练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >三定点A(2,1)B(0,-1)C(-2,1),三动点DEM满足AD=tAB,BE=tBC,DM=tDE,t属于[0,1], 10

    三定点A(2,1)B(0,-1)C(-2,1),三动点DEM满足AD=tAB,BE=tBC,DM=tDE,t属于[0,1], 10答案解析

    科目：gzsx 来源： 题型：

    如图，在双曲线-=1的上支上有三点A(x1,y1),B(x2,6),C(x3,y3),它们与点F(0,5)的距离成等差数列.

    (1)求y1+y3的值；

    (2)证明线段AC的垂直平分线经过某一定点，并求此点坐标.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

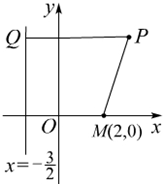    已知平面直角坐标系xOy上的定点M（2，0）和定直线l：x=-
    3
    2
    ，动点P在直线l上的射影为Q，且4(
    PQ
    +
    PM
    )•(
    PQ
    -
    PM
    )+2
    PM
    •
    OM
    =1    ．
    （1）求点P的轨迹C的方程；
    （2）设A、B是轨迹C上两个动点，
    MA
    =λ
    MB
    ，λ∈R，∠AOB=θ，请把△AOB的面积S表示为θ的函数，并求此函数的定义域．

    查看答案和解析>>

    科目：gzsx 来源：四川省成都市龙泉中学2010届高三第五次调研考试数学理科试题 题型：022

    有以下几个命题

    ①若函数是连续函数，则的值是±1；

    ②由一组样本数据(x1，y1)，(x2，y2)，…，(xn，yn)得到的回归直线方程为，直线必经过点；

    ③设A、B为两个定点，m(m＞0)为常数，，则动点P的轨迹为椭圆；

    ④若数列{an}是递增数列，且an＝n2＋λn＋1(n≥2，n∈N*)，则实数λ的取值范围

    是(－5，＋∞)；

    ⑤若椭圆的左、右焦点分别为F1、F2，P是该椭圆上的任意一点，则点F2关于∠F1PF2的外角平分线对称的点M的轨迹是圆．

    其中真命题的序号为________；(写出所有真命题的序号)

    查看答案和解析>>

    科目：gzsx 来源：四川省成都市龙泉中学2010届高三第五次调研考试数学文科试题 题型：022

    有以下几个命题

    ①一个容量为n的样本，分成若干组，已知某组的频数和频率分别为40和0.125，则n的值为320；

    ②设A、B为两个定点，m(m＞0)为常数，，则动点P的轨迹为椭圆；

    ③若数列{an}是递增数列，且an＝n2＋λn＋1(n≥2，n∈N*)，则实数λ的取值范围是(－5，＋∞)；

    ④若椭圆的左、右焦点分别为F1、F2，P是该椭圆上的任意一点，则点F2关于∠F1PF2的外角平分线对称的点M的轨迹是圆．

    其中真命题的序号为________；(写出所有真命题的序号)

    查看答案和解析>>

    科目：gzsx 来源： 题型：解答题

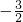    已知平面直角坐标系xOy上的定点M（2，0）和定直线l：x=数学公式，动点P在直线l上的射影为Q，且4数学公式．
    （1）求点P的轨迹C的方程；
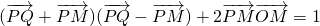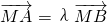    （2）设A、B是轨迹C上两个动点，数学公式，λ∈R，∠AOB=θ，请把△AOB的面积S表示为θ的函数，并求此函数的定义域．

    查看答案和解析>>

    科目：gzsx 来源：2011年河北省唐山一中高考数学仿真试卷3（文科）（解析版） 题型：解答题

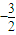    已知平面直角坐标系xOy上的定点M（2，0）和定直线l：x=，动点P在直线l上的射影为Q，且4．
    （1）求点P的轨迹C的方程；
    （2）设A、B是轨迹C上两个动点，，λ∈R，∠AOB=θ，请把△AOB的面积S表示为θ的函数，并求此函数的定义域．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2007•闵行区一模）（理）已知△ABC顶点的直角坐标分别为A（a，4）、B（0，b）、C（c，0）．
    （1）若a=3，b=0，c=5，求sinA的值；
    （2）若虚数x=2+ai（a＞0）是实系数方程x2-cx+5=0的根，且∠A是钝角，求b的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知点P（-1，
    3
    2
    ）是椭圆C：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）上一点F1、F2分别是椭圆C的左、右焦点，O是坐标原点，PF1⊥x轴．
    ①求椭圆C的方程；
    ②设A、B是椭圆C上两个动点，满足：
    PA
    +
    PB
    =λ
    PO
    （0＜λ＜4，且λ≠2）求直线AB的斜率．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知直线l过点（0，
    5
    4
    ），且斜率为
    1
    2
    ，抛物线C：y2=2px（p大于0）的顶点关于直线l的对称点在该抛物线的准线上．
    （1）求抛物线C的方程；
    （2）设A、B是抛物线C上两个动点，过A作平行于x轴的直线m，直线OB与直线m交于点N，若
    OA
    ．
    OB
    +P2=0    （O为原点，A、B异于原点），试求点N的轨迹方程．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知点P（-1，
    3
    2
    ）是椭圆C：
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）上一点F1、F2分别是椭圆C的左、右焦点，O是坐标原点，PF1⊥x轴．
    ①求椭圆C的方程；
    ②设A、B是椭圆C上两个动点，满足
    PA
    +
    PB
    =λ
    PO
    （0＜λ＜4，且λ≠2）求直线AB的斜率．

    查看答案和解析>>

    科目：gzsx 来源：2013届河北省高二上学期期中理科数学试卷 题型：选择题

    若直线与圆没有交点，则过点的直线与椭圆的公共点个数为(   )

    A.至少一个      B.0个         C.1个          D.2个

     

    查看答案和解析>>

    科目：gzsx 来源：2013届山东省济宁市高二3月月考理科数学试卷 题型：选择题

    若直线与圆没有交点，则过点的直线与椭圆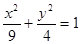的公共点个数为（   ）

    A.至少一个          B.0个               C.1个          D.2个

     

    查看答案和解析>>

    科目：gzsx 来源：2014届浙江省宁波市高一下期中数学试卷（解析版） 题型：选择题

    的三个内角为，的最大值是 (     )

    A．3          B.0.5             C．1          D．1.5

     

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知以向量v=为方向向量的直线l过点，抛物线C：y2=2px（p＞0）的顶点关于直线l的对称点在该抛物线的准线上.

    （1）求抛物线C的方程；

    （2）设A、B是抛物线C上两个动点，过A作平行于x轴的直线m,直线OB与直线m交于点N，若·+p2=0 （O为原点，A、B异于原点），试求点N的轨迹方程.

    查看答案和解析>>

    科目：gzsx 来源：2008年上海市闵行区高考数学一模试卷（文理合卷）（解析版） 题型：解答题

    （理）已知△ABC顶点的直角坐标分别为A（a，4）、B（0，b）、C（c，0）．
    （1）若a=3，b=0，c=5，求sinA的值；
    （2）若虚数x=2+ai（a＞0）是实系数方程x2-cx+5=0的根，且∠A是钝角，求b的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知以向量v=(1,)为方向向量的直线l过点(0,),抛物线C:y2=2px(p＞0)的顶点关于直线l的对称点在该抛物线的准线上.

    (1)求抛物线C的方程;

    (2)设A、B是抛物线C上两个动点,过A作平行于x轴的直线m,直线OB与直线m交于点N,若+p2=0(O为原点,A、B异于原点),试求点N的轨迹方程.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设函数f(x)=(1+x)2-2ln(1+x).

    (1)求函数f(x)的单调区间;

    (2)当0＜a＜2时,求函数g(x)=f(x)-x2-ax-1在区间［0,3］上的最小值.

    (文)已知向量a=(cosx,cosx),b=(0,sinx),c=(sinx,cosx),d=(sinx,sinx).

    (1)当x=时,求向量a、b的夹角;

    (2)当x∈［0,］时,求c·d的最大值;

    (3)设函数f(x)=(a-b)·(c+d),将函数f(x)的图象按向量m平移后得到函数g(x)的图象,且g(x)=2sin2x+1,求|m|的最小值.

    查看答案和解析>>

    科目：gzsx 来源：2010年广东省广州市越秀区高考数学一轮双基小题练习（10）（解析版） 题型：解答题

    已知直线l过点（0，），且斜率为，抛物线C：y2=2px（p大于0）的顶点关于直线l的对称点在该抛物线的准线上．
    （1）求抛物线C的方程；
    （2）设A、B是抛物线C上两个动点，过A作平行于x轴的直线m，直线OB与直线m交于点N，若（O为原点，A、B异于原点），试求点N的轨迹方程．

    查看答案和解析>>

    科目：gzsx 来源：闵行区一模 题型：解答题

    （理）已知△ABC顶点的直角坐标分别为A（a，4）、B（0，b）、C（c，0）．
    （1）若a=3，b=0，c=5，求sinA的值；
    （2）若虚数x=2+ai（a＞0）是实系数方程x2-cx+5=0的根，且∠A是钝角，求b的取值范围．

    查看答案和解析>>

    科目：gzsx 来源：2010年江苏省徐州一中高三数学提优练习（14）（解析版） 题型：解答题

    已知直线l过点（0，），且斜率为，抛物线C：y2=2px（p大于0）的顶点关于直线l的对称点在该抛物线的准线上．
    （1）求抛物线C的方程；
    （2）设A、B是抛物线C上两个动点，过A作平行于x轴的直线m，直线OB与直线m交于点N，若（O为原点，A、B异于原点），试求点N的轨迹方程．

    查看答案和解析>>