
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 1 |
| 4 |
科目:gzsx 来源: 题型:
| ||
| 2 |
| 1 |
| 4 |
科目:gzsx 来源:2012-2013学年山东省济宁市鱼台一中高三(上)期末数学模拟试卷(理科)(解析版) 题型:解答题
 的左、右两个焦点,若椭圆C上的点A(1,
的左、右两个焦点,若椭圆C上的点A(1, )到F1,F2两点的距离之和等于4.
)到F1,F2两点的距离之和等于4. )的直线与椭圆交于两点D、E,若DP=PE,求直线DE的方程;
)的直线与椭圆交于两点D、E,若DP=PE,求直线DE的方程;科目:gzsx 来源:不详 题型:解答题
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 1 |
| 4 |
科目:gzsx 来源:2012-2013学年辽宁省沈阳二中等重点中学协作体高考预测数学试卷10(理科)(解析版) 题型:解答题
 的左、右两个焦点,若椭圆C上的点A(1,
的左、右两个焦点,若椭圆C上的点A(1,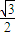 )到F1,F2两点的距离之和等于4.
)到F1,F2两点的距离之和等于4. )的直线与椭圆交于两点D、E,若DP=PE,求直线DE的方程;
)的直线与椭圆交于两点D、E,若DP=PE,求直线DE的方程;科目:gzsx 来源: 题型:解答题
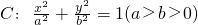 的左、右两个焦点,若椭圆C上的点A(1,
的左、右两个焦点,若椭圆C上的点A(1, )到F1,F2两点的距离之和等于4.
)到F1,F2两点的距离之和等于4. )的直线与椭圆交于两点D、E,若DP=PE,求直线DE的方程;
)的直线与椭圆交于两点D、E,若DP=PE,求直线DE的方程;科目:gzsx 来源:2012-2013学年江西省赣州市于都实验中学高三(上)第三次月考数学试卷(理科)(解析版) 题型:解答题
 的左、右两个焦点,若椭圆C上的点A(1,
的左、右两个焦点,若椭圆C上的点A(1, )到F1,F2两点的距离之和等于4.
)到F1,F2两点的距离之和等于4. )的直线与椭圆交于两点D、E,若DP=PE,求直线DE的方程;
)的直线与椭圆交于两点D、E,若DP=PE,求直线DE的方程;科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 3 |
| 2 |
科目:gzsx 来源:2013年甘肃省定西市文峰中学高三新课标数学模拟试卷(二)(解析版) 题型:解答题
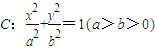 的左、右两个焦点,若椭圆C上的点
的左、右两个焦点,若椭圆C上的点 两点的距离之和等于4.
两点的距离之和等于4. )的直线与椭圆交于两点M、N,若OM⊥ON,求直线MN的方程.
)的直线与椭圆交于两点M、N,若OM⊥ON,求直线MN的方程.科目:gzsx 来源:不详 题型:解答题
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 3 |
| 2 |
科目:gzsx 来源:湖南省岳阳市一中2009届高三第七次月考数学(文)试题 题型:044
设F1,F2分别为椭圆![]() (a>b>0)的左、右两个焦点,若椭圆C上的点A
(a>b>0)的左、右两个焦点,若椭圆C上的点A![]() 到F1,F2两点的距离之和等于4.
到F1,F2两点的距离之和等于4.
(1)求出椭圆C的方程和焦点坐标;
(2)过点P(0,![]() )的直线与椭圆交于两点M、N,若以MN为直径的圆通过原点,求直线MN的方程.
)的直线与椭圆交于两点M、N,若以MN为直径的圆通过原点,求直线MN的方程.
科目:gzsx 来源: 题型:
设![]() 分别为椭圆
分别为椭圆![]() 的左、右两个焦点,若椭圆C上的点A(1,
的左、右两个焦点,若椭圆C上的点A(1,![]() )到F1,F2两点的距离之和等于4.
)到F1,F2两点的距离之和等于4.
⑴写出椭圆C的方程和焦点坐标;
⑵过点P(1,![]() )的直线与椭圆交于两点D、E,若DP=PE,求直线DE的方程;
)的直线与椭圆交于两点D、E,若DP=PE,求直线DE的方程;
⑶过点Q(1,0)的直线与椭圆交于两点M、N,若△OMN面积取得最大,求直线MN的方程.
科目:gzsx 来源:2013-2014学年福建泉州五中、莆田、漳州一中高三上期末理数学卷(解析版) 题型:解答题
已知椭圆 :
: 的左焦点为
的左焦点为 ,且过点
,且过点 .
.

(1)求椭圆 的方程;
的方程;
(2)设过点P(-2,0)的直线与椭圆E交于A、B两点,且满足 .
.
①若 ,求
,求 的值;
的值;
②若M、N分别为椭圆E的左、右顶点,证明: 
科目:gzsx 来源: 题型:
已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,若以
,若以![]() 为圆心,
为圆心,![]() 为半径作圆
为半径作圆![]() ,过椭圆上一点
,过椭圆上一点![]() 作此圆的切线,切点为
作此圆的切线,切点为![]() ,且
,且![]() 的最小值不小于为
的最小值不小于为![]() .
.
(1)求椭圆的离心率![]() 的取值范围;
的取值范围;
(2)设椭圆的短半轴长为![]() ,圆
,圆![]() 与
与![]() 轴的右交点为
轴的右交点为![]() ,过点
,过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与椭圆相交于
与椭圆相交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得的弦长
截得的弦长![]() 的最大值.
的最大值.
科目:gzsx 来源:2007-2008学年江苏省南通市启东中学高三(上)期末数学复习试卷1(解析版) 题型:解答题
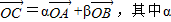 、β∈R,且α-2β=1
、β∈R,且α-2β=1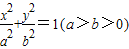 交于两点M、N,且以MN为直径的圆过原点,求证:
交于两点M、N,且以MN为直径的圆过原点,求证: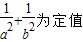 ;
; ,求椭圆长轴长的取值范围.
,求椭圆长轴长的取值范围.科目:gzsx 来源:2008-2009学年重庆市西南师大附中高三(上)2月月考数学试卷(文科)(解析版) 题型:解答题
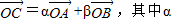 、β∈R,且α-2β=1
、β∈R,且α-2β=1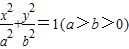 交于两点M、N,且以MN为直径的圆过原点,求证:
交于两点M、N,且以MN为直径的圆过原点,求证: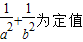 ;
;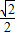 ,求椭圆长轴长的取值范围.
,求椭圆长轴长的取值范围.科目:gzsx 来源:2011-2012学年四川省高考压轴理科数学试卷(解析版) 题型:解答题
(本小题满分14分)(注意:在试题卷上作答无效)
已知椭圆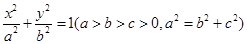 的左、右焦点分别为
的左、右焦点分别为 ,若以
,若以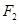 为圆心,
为圆心, 为半径作圆
为半径作圆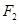 ,过椭圆上一点
,过椭圆上一点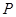 作此圆的切线,切点为
作此圆的切线,切点为 ,且
,且 的最小值不小于为
的最小值不小于为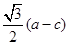 .
.
(1)求椭圆的离心率 的取值范围;
的取值范围;
(2)设椭圆的短半轴长为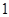 ,圆
,圆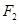 与
与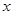 轴的右交点为
轴的右交点为 ,过点
,过点 作斜率为
作斜率为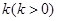 的直线
的直线 与椭圆相交于
与椭圆相交于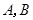 两点,若
两点,若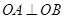 ,求直线
,求直线 被圆
被圆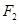 截得的弦长
截得的弦长 的最大值.
的最大值.
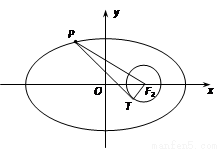
科目:gzsx 来源:2012-2013学年湖南省元月考文科数学试卷(解析版) 题型:解答题
(本小题满分13分)已知点 分别为椭圆
分别为椭圆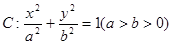 的左、右焦点,点
的左、右焦点,点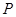 为椭圆上任意一点,
为椭圆上任意一点,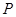 到焦点
到焦点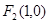 的距离的最大值为
的距离的最大值为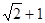 .
.
(1)求椭圆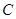 的方程。
的方程。
(2)点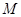 的坐标为
的坐标为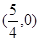 ,过点
,过点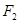 且斜率为
且斜率为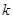 的直线
的直线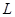 与椭圆
与椭圆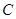 相交于
相交于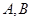 两点。对于任意的
两点。对于任意的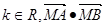 是否为定值?若是求出这个定值;若不是说明理由。
是否为定值?若是求出这个定值;若不是说明理由。
科目:gzsx 来源:2011-2012学年山东省青州市高三2月月考理科数学 题型:解答题
已知点 分别为椭圆
分别为椭圆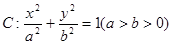 的左、右焦点,点
的左、右焦点,点 为椭圆上任意一点,
为椭圆上任意一点, 到焦点
到焦点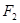 的距离的最大值为
的距离的最大值为 ,且
,且 的最大面积为
的最大面积为 .
.
(I)求椭圆 的方程。
的方程。
(II)点 的坐标为
的坐标为 ,过点
,过点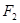 且斜率为
且斜率为 的直线
的直线 与椭圆
与椭圆 相交于
相交于 两点。对于任意的
两点。对于任意的 是否为定值?若是求出这个定值;若不是说明理由。
是否为定值?若是求出这个定值;若不是说明理由。
科目:gzsx 来源:2012-2013学年甘肃省兰州市高三第一次(3月)诊断考试理科数学试卷(解析版) 题型:解答题
已知点 为
为 轴上的动点,点
轴上的动点,点 为
为 轴上的动点,点
轴上的动点,点 为定点,且满足
为定点,且满足 ,
, .
.
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过点 且斜率为
且斜率为 的直线
的直线 与曲线
与曲线 交于两点
交于两点 ,
, ,试判断在
,试判断在 轴上是否存在点
轴上是否存在点 ,使得
,使得 成立,请说明理由.
成立,请说明理由.