
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
| 1 | 3 |

科目:czsx 来源: 题型:
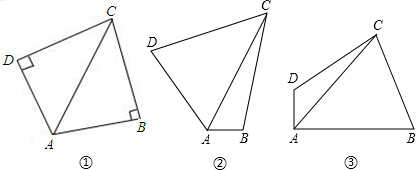
科目:czsx 来源: 题型:
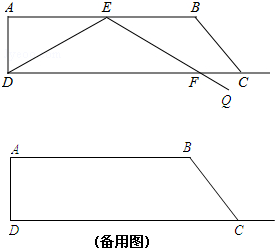 (2013•历城区一模)如图,在直角梯形ABCD中,∠A=90°,∠B=120°,AD=
(2013•历城区一模)如图,在直角梯形ABCD中,∠A=90°,∠B=120°,AD=| 3 |
科目:czsx 来源: 题型:
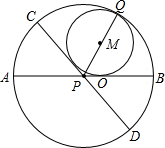 Q分别为PB、弧CQB上的切点.
Q分别为PB、弧CQB上的切点.科目:czsx 来源: 题型:
如图,八一广场要设计一个矩形花坛,花坛的长、宽分别为200 m、
120 m,花坛中有一横两纵的通道,横、纵通道的宽度分别为3x m、2x m.

(1)用代数式表示三条通道的总面积S;当通道总面积为花坛总面积的![]() 时,求横、纵通道的宽分别是多少?
时,求横、纵通道的宽分别是多少?
(2)如果花坛绿化造价为每平方米3元,通道总造价为3168 x元,那么横、纵通道的宽分别为多少米时,花坛总造价最低?并求出最低造价.
(以下数据可供参考:852 = 7225,862 = 7396,872 = 7569)
科目:czsx 来源: 题型:

 时,求横、纵通道的宽分别是多少?
时,求横、纵通道的宽分别是多少?科目:czsx 来源:2011—2012学年山东潍坊八年级下期末模拟数学试卷(带解析) 题型:解答题
一司机驾驶汽车从甲地去乙地,以80千米/小时的平均速度用6小时到达目的地.
(1)当他按原路匀速返回时,求汽车速度v(千米/小时)与时间t(小时)之间的函数关系式;
(2)如果该司机匀速返回时,用了4.8小时,求返回时的速度;
(3)若返回时,司机全程走高速公路,且匀速行驶,根据规定:最高车速不得超过每小时120公里,最低车速不得低于每小时60公里,试问返程时间的范围是多少?
科目:czsx 来源:2011-2012学年山东潍坊八年级下期末模拟数学试卷(解析版) 题型:解答题
一司机驾驶汽车从甲地去乙地,以80千米/小时的平均速度用6小时到达目的地.
(1)当他按原路匀速返回时,求汽车速度v(千米/小时)与时间t(小时)之间的函数关系式;
(2)如果该司机匀速返回时,用了4.8小时,求返回时的速度;
(3)若返回时,司机全程走高速公路,且匀速行驶,根据规定:最高车速不得超过每小时120公里,最低车速不得低于每小时60公里,试问返程时间的范围是多少?
科目:czsx 来源:2013年山东省济南市历城中考一模数学试卷(解析版) 题型:解答题
如图,在直角梯形ABCD中,∠A=90°,∠B=120°,AD= ,AB=6.在底边AB上有一动点E,满足∠DEQ=120°,EQ交射线DC于点F.
,AB=6.在底边AB上有一动点E,满足∠DEQ=120°,EQ交射线DC于点F.

(1)求下底DC的长度;
(2)当点E是AB的中点时,求线段DF的长度;
(3)请计算射线EF经过点C时,AE的长度.
科目:czsx 来源:2013年山东省济南市历城中考一模数学试卷(带解析) 题型:解答题
如图,在直角梯形ABCD中,∠A=90°,∠B=120°,AD=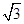 ,AB=6.在底边AB上有一动点E,满足∠DEQ=120°,EQ交射线DC于点F.
,AB=6.在底边AB上有一动点E,满足∠DEQ=120°,EQ交射线DC于点F.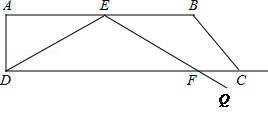
(1)求下底DC的长度;
(2)当点E是AB的中点时,求线段DF的长度;
(3)请计算射线EF经过点C时,AE的长度.
科目:czsx 来源:2010年高级中等学校招生全国统一考试数学卷(辽宁沈阳) 题型:解答题
如图,八一广场要设计一个矩形花坛,花坛的长、宽分别为200 m、
120 m,花坛中有一横两纵的通道,横、纵通道的宽度分别为3x m、2x m.
(1)用代数式表示三条通道的总面积S;当通道总面积为花坛总面积的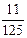 时,求横、纵通道的宽分别是多少?
时,求横、纵通道的宽分别是多少?
(2)如果花坛绿化造价为每平方米3元,通道总造价为3168 x元,那么横、纵通道的宽分别为多少米时,花坛总造价最低?并求出最低造价.
(以下数据可供参考:852 = 7225,862 = 7396,872 = 7569)
科目:czsx 来源:2010年高级中等学校招生全国统一考试数学卷(辽宁沈阳) 题型:解答题
如图,八一广场要设计一个矩形花坛,花坛的长、宽分别为200 m、
120 m,花坛中有一横两纵的通道,横、纵通道的宽度分别为3x m、2x m.
(1)用代数式表示三条通道的总面积S;当通道总面积为花坛总面积的 时,求横、纵通道的宽分别是多少?
时,求横、纵通道的宽分别是多少?
(2)如果花坛绿化造价为每平方米3元,通道总造价为3168 x元,那么横、纵通道的宽分别为多少米时,花坛总造价最低?并求出最低造价.
(以下数据可供参考:852 = 7225,862 = 7396,872 = 7569)
科目:czsx 来源: 题型:
如图,八一广场要设计一个矩形花坛,花坛的长、宽分别为200 m、120 m,花坛中有一横两纵的通道,横、纵通道的宽度分别为3x m、2x m.
(1)用代数式表示三条通道的总面积S;当通道总面积为花坛总面积的![]() 时,求横、纵通道的宽分别是多少?
时,求横、纵通道的宽分别是多少?
(2)如果花坛绿化造价为每平方米3元,通道总造价为3168 x元,那么横、纵通道的宽分别为多少米时,花坛总造价最低?并求出最低造价.(以下数据可供参考:852 = 7225,862 = 7396,872 = 7569)
 |
科目:czsx 来源:2012年江苏省扬州市宝应县望直港中学中考数学二模试卷(解析版) 题型:解答题
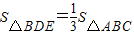 时,求AD的长.
时,求AD的长.
科目:czsx 来源:2011年上海市普陀区中考数学二模试卷(解析版) 题型:解答题
 时,求AD的长.
时,求AD的长.
科目:czsx 来源:2010年四川省绵阳市高级中等教育学校招生统一考试数学试题 题型:044
如图,八一广场要设计一个矩形花坛,花坛的长、宽分别为200 m、120 m,花坛中有一横两纵的通道,横、纵通道的宽度分别为3x m、2x m.
(1)用代数式表示三条通道的总面积S;当通道总面积为花坛总面积的![]() 时,求横、纵通道的宽分别是多少?
时,求横、纵通道的宽分别是多少?
(2)如果花坛绿化造价为每平方米3元,通道总造价为3168x元,
那么横、纵通道的宽分别为多少米时,花坛总造价最低?并求出最低造价.
(以下数据可供参考:852=7225,862=7396,872=7569)