练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >8年级数学上册试题

    8年级数学上册试题答案解析

    科目：czsx 来源： 题型：

    教材在七年级数学（上册）的第20页介绍了填幻方，这部分内容就是传说的“龟背图”，也就是“九宫图”．根据所给的“九宫图”请你找找规律，利用发现的规律将3，5，-7，1，7，-3，9，-5，-1这九个数字分别填入图中的九个方格中，使得横、竖、斜对角的所有三个数的和相等．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    教材在七年级数学（上册）的第20页介绍了填幻方，这部分内容就是传说的“龟背图”，也就是“九宫图”．根据所给的“九宫图”请你找找规律，利用发现的规律将3，5，-7，1，7，-3，9，-5，-1这九个数字分别填入图中的九个方格中，使得横、竖、斜对角的所有三个数的和相等．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （2013•本溪）校车安全是近几年社会关注的热点问题，安全隐患主要是超速和超载．某中学九年级数学活动小组进行了测试汽车速度的实验，如图，先在笔直的公路l旁选取一点A，在公路l上确定点B、C，使得AC⊥l，∠BAC=60°，再在AC上确定点D，使得∠BDC=75°，测得AD=40米，已知本路段对校车限速是50千米/时，若测得某校车从B到C匀速行驶用时10秒，问这辆车在本路段是否超速？请说明理由（参考数据：
    		2
    =1.41，
    		3
    =1.73）

    查看答案和解析>>

    科目：czsx 来源： 题型：

    18、至诚学校初一年级数学竞赛，得100分的有2人，90～99分的有9人，80～89分的有17人，70～79分的有28人，60～69分的有36人，50～59分的有7人，还有1人得48分，则总平均成绩介于
    68.88
    分（最小值）与
    77.61
    分（最大值）之间．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    22、某学校组织学生参加全市七年级数学竞赛，22名同学获市一等奖和市二等奖，为鼓励这些同学，学校准备拿出2000元资金给这些获奖学生买奖品，一等奖每人200元，二奖等奖每人50元，求得到一等奖和二等奖的学生分别是多少人？

    查看答案和解析>>

    科目：czsx 来源： 题型：

    为了了解本次考试九年级数学成绩情况，以九年级（1）班学生的成绩为样本，按A，B，C，D四个等级进行统计，并将结果制成如下两幅统计图，请你根据图中所给信息完成下列各题：
    （1）求出扇形统计图中C级所在的扇形圆心角的度数．
    （2）求出D级学生的人数占全班人数的百分比．
    （3）若我校九年级共有1500人你估计一下，在这次考试中A级和B级共有多少人？

    查看答案和解析>>

    科目：czsx 来源： 题型：

    某学校七年级数学兴趣小组组织一次数学活动．在一座有三道环形路的数字迷宫的每个进口处都标记着一个数，要求进入者把自己当做数“1”，进入时必须乘进口处的数，并将结果带到下一个进口，依次累乘下去，在通过最后一个进口时，只有乘积是5的倍数，才可以进入迷宫中心，现让一名5岁小朋友小军从最外环任一个进口进入．
    （1）小军能进入迷宫中心的概率是多少？请画出树状图进行说明；
    （2）小组两位组员小张和小李商量做一个小游戏，以猜测小军进迷宫的结果比胜负．游戏规则规完：小军如果能进入迷宫中心，小张和小李各得1分；小军如果不能进入迷宫中心，则他在最后一个进口处所得乘积是奇数时，小张得3分，所得乘积是偶数时，小李得3分，你认为这个游戏公平吗？如果公平，请说明理由；如果不公平，请在第二道环进口处的两个数中改变其中一个数使游戏公平．
    （3）在（2）的游戏规则下，让小军从最外环进口任意进入10次，最终小张和小李的总得分之和不超过28分精英家教网，请问小军至少几次进入迷宫中心？

    查看答案和解析>>

    科目：czsx 来源： 题型：

    7、某次考试初一年级数学平均分为73分，其中最高分高出平均分25分，最低分比平均分低24分，请问最高分比最低分高
    49
    分．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    在一次九年级数学测试中，九（1）班的平均成绩为79.5，标准差为24，优秀率（≥90分为优秀）25%，及格率为85%，中位数为81；九（2）班的平均成绩为80.2，标准差为15，优秀率20%，及格率为88%，中位数为79．
    （1）从两个角度评价两个班的成绩；
    （2）复核时老师发现改错一道3分的选择题．校正后统计：九（1）班有60%的人要加3分，20%的人要减3分，20%的人不变；而九（2）班有50%的人要加3分，30%的人要减3分，20%的人不变．刘星同学说校正后九（1）班的平均成绩会超过九（2）班，你认为正确吗？请说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （1）人教版八年级数学下册92页第14题是这样叙述的：如图1，▱ABCD中，过对角线BD上一点P作EF∥BC，HG∥AB，图中哪两个平行四边形的面积相等？为什么？
    根据习题背景，写出面积相等的一对平行四边形的名称为
    ▱AEPH
    ▱AEPH
    和
    ▱PGCF
    ▱PGCF
    ；
    （2）如图2，点P为▱ABCD内一点，过点P分别作AD、AB的平行线分别交▱ABCD的四边于点E、F、G、H．已知S▱BHPE=3，S▱PFDG=5，则S△PAC=
    1
    1
    ；
    （3）如图3，若①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH（不重复、无缝隙）．已知①②③④四个平行四边形面积的和为14，四边形ABCD的面积为11，则菱形EFGH的周长为
    24
    24
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （1）已知a=2，b=-1，求1+
    a2-b2
    a2-ab
    ÷
    1
    a
    的值．
    （2）某校九年级数学兴趣小组的同学开展了测量闽江宽度的活．如图，他们在河东岸边的点A测得河西岸边的标志物B在它的正西方向，然后从点A出发沿河岸向正北方向行进550 m到点C处，测得B在点C的南偏西60°方向上，他们测得的闽江宽度是多少米？（结果保留整数，参考数据：
    		2
    ≈1.414，
    		3
    ≈l.732）
    精英家教网

    查看答案和解析>>

    科目：czsx 来源： 题型：

    为了了解某中学初三年级250名学生升学考试的数学成绩，从中抽取了50名学生的数学成绩进行分析，求得
    .
    x
    样本=93.5．下面是50名学生数学成绩的频率分布表：
     分组  频数累计  频数  频率
     60.5～70.5  正  3  a
     70.5～80.5  正正  6  0.12
     80.5～90.5  正正  9  0.18
     90.5～100.5  正正正正  17  0.34
     100.5～110.5  正正  b  0.2
     110.5～120.5  正  5  0.1
     合计    50  1
    根据题中给出的条件回答下列问题：
    （1）在这次抽样分析的过程中，样本是
     
    ；
    （2）频率分布表中的数据a=
     
    b=
     
    ；
    （3）估计该校初三年级这次升学考试的数学平均成绩约为
     
    分；
    （4）在这次升学考试中，该校初三年级数学成绩在90.5～100.5范围内的人数约为
     
    人．

    查看答案和解析>>

    科目：czsx 来源： 题型：

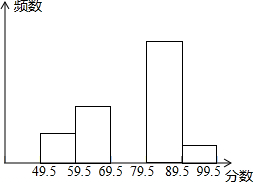    为了配合数学课程改革，某县举行了初三年级“数学知识应用”竞赛（满分100分）．为了解初三年级参赛的1万名学生竞赛成绩情况，现从中随机抽取部分学生的竞赛成绩作为一个样本，整理后分成5组，绘制出频数分布直方图．已知图中从左到右的第一、第二、第四、第五小组的频数分别是50，100，200，25，其中第二小组的精英家教网频率是0.2．
    （1）求第三小组的频数，并补全频数分布直方图；
    （2）抽取的样本中，学生竞赛成绩的中位数落在第几小组？
    （3）若成绩在90分以上（含90分）的学生获优胜奖，请你估计全县初三参赛学生中获优胜奖的人数．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    14、印有“八年级数学卷”字样的立方体，其中一个立方体表面展开图如图所示，则与印有“数”字面相对的表面上印有
    卷
    字．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    16、乐乐学了七年级数学第二章《有理数及其运算》之后，总结出下列结论：①相反数等于本身的有理数只有0；②倒数等于本身的有理数只有1；③0和正数的绝对值都是它本身；④立方等于本身的有理数有3个．其中，你认为正确结论的序号是
    ①③④
    （多填或错填的得0分，少填的酌情给分）．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    某校为了奖励在七年级数学竞赛中获奖的学生，买了若干本课外读物准备奖给他们，若每人奖3本，则余8本；若前面每人奖5本，则最后一人奖得的课外读物不足3本．该校有多少名学生获奖？买了多少本课外读物？

    查看答案和解析>>

    科目：czsx 来源： 题型：

    八年级数学学习小组的同学就全校同学在暑假期间有意向参观“2010年上海世博会”的人数进行了统计．第一次统计时，有意向者475人，到第三次统计时，有意向者达到684人，则有意向者平均每次的增长率为
    20%
    20%
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

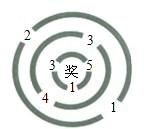    如图，某学校九年级数学兴趣小组组织一次数学活动．在一座有三道环形路的数字迷宫的每个进口处都标记着一个数，要求进入者把自己当做数“1”，进入时必须乘进口处的数，并将结果带到下一个进口，依次累乘下去，在通过最后精英家教网一个进口时，只有乘积是3的倍数，才可以进入迷宫中心，现让小军从最外环任一个进口进入．
    （1）小军能进入迷宫中心的概率是多少？请画出树状图进行说明．
    （2）小组两位组员小张和小李商量做一个小游戏，以猜测小军进迷宫的结果比胜负．游戏规则规下：小军如能进入迷宫中心，小张得1分；小军如不能进入迷宫中心，则小李得2分．你认为这个游戏公平吗？请说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：

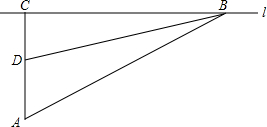
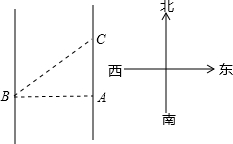
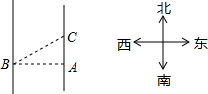    （2011•河源）某校九年级数学兴趣小组的同学开展了测量东江宽度的活动．如图，他们在河东岸边的A点测得河西岸边的标志物B在它的正西方向，然后从A点出发沿河岸向正北方向行进200米到点C处，测得B在点C的南偏西60° 的方向上，他们测得东江的宽度是多少米？（结果保留整数，参考数据：
    		2
    ≈1.414，
    		3
    ≈1.732    ）

    查看答案和解析>>

    科目：czsx 来源： 题型：

    九年级数学兴趣小组组织了以“等积变形”为主题的课题研究．
    第一学习小组发现：如图（1），点A、点B在直线l1上，点C、点D在直线l2上，若l1∥l2，则S△ABC=S△ABD；反之亦成立．
    第二学习小组发现：如图（2），点P是反比例函数y=
    k
    x
    上任意一点，过点P作x轴、y轴的垂线，垂足为M、N，则矩形OMPN的面积为定值|k|．
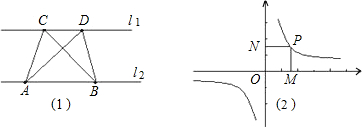
    精英家教网
    请利用上述结论解决下列问题：
    （1）如图（3），四边形ABCD、与四边形CEFG都是正方形点E在CD上，正方形ABCD边长为2，则S△BDF=
     
    ．
    （2）如图（4），点P、Q在反比例函数y=
    k
    x
    图象上，PQ过点O，过P作y轴的平行线交x轴于点H，过Q作x轴的平行线交PH于点G，若S△PQG=8，则S△POH=
     
    ，k=
     
    ．
    （3）如图（5）点P、Q是第一象限的点，且在反比例函数y=
    k
    x
    图象上，过点P作x轴垂线，过点Q作y轴垂线，垂足分别是M、N，试判断直线PQ与直线MN的位置关系，并说明理由．
    精英家教网

    查看答案和解析>>