已知关于X的一元二次方程X的平方减6X加2M减1=0有两个相等的实数根答案解析
科目：czsx
来源：
题型：
已知关于x的一元二次方程kx
2-2（k+1）x+k-1=0有两个不相等的实数根x
1，x
2．
（1）求k的取值范围；
（2）是否存在实数k，使
+
=1成立？若存在，请求出k的值；若不存在，请说明理由．
查看答案和解析>>
科目：czsx
来源：
题型：
已知关于x的一元二次方程mx
2-2x+1=0．
（1）若方程有两个实数根，求m的范围；
（2）若方程的两个实数根为x
1、x
2，x
1•x
2-x
1-x
2=
，求m的值．
查看答案和解析>>
科目：czsx
来源：
题型：
已知关于x的一元二次方程x2+2（k-1）x+k2-1=0有两个不相等的实数根．
（1）求实数k的取值范围；
（2）若方程的一个根是0，求出它的另一个根及k的值．
查看答案和解析>>
科目：czsx
来源：
题型：
已知关于x的一元二次方程x2-2x+k=0．
（1）当方程有两个实数根时，求实数k的取值范围；
（2）当方程无实数根时，求实数k的取值范围．
查看答案和解析>>
科目：czsx
来源：
题型：
已知关于x的一元二次方程x2+2（k-1）x+k2-1=0有两个不相等的实数根．求实数k的取值范围．
查看答案和解析>>
科目：czsx
来源：
题型：
已知关于x的一元二次方程x2+2（k-1）x+k2-1=0有两个不相等的实数根x1，x2．
（1）求实数k的取值范围；
（2）若3（x1+x2）=x1x2，求k的值．
查看答案和解析>>
科目：czsx
来源：
题型：
已知关于x的一元二次方程2x2-5x-a=0
（1）如果此方程有两个不相等的实数根，求a的取值范围．
（2）当a为何值时，方程的两个根互为倒数，求出此时方程的解．
查看答案和解析>>
科目：czsx
来源：
题型：
（2005•闸北区二模）已知关于x的一元二次方程x2-4x+m=0．
（1）如果方程有两个实数根，求m的取值范围；
（2）设方程的两个实数根为x1和x2，如果（x1-2）（x2-2）=5m，求m的值．
查看答案和解析>>
科目：czsx
来源：
题型：
21、已知关于x的一元二次方程x2+2（k-1）x+k2-1=0有两个不相等的实数根．
（1）求实数k的取值范围；
（2）0可能是方程的一个根吗？若是，请求出它的另一个根；若不是，请说明理由．
查看答案和解析>>
科目：czsx
来源：
题型：
已知：关于x的一元二次方程ax2+2（a-3）x+a+3=0有两个实数根，且a为非负整数．
（1）求a的值；
（2）若抛物线y=ax2+2（a-3）x+a+3向下平移m（m＞0）个单位后过点（1，n）和点（2，2n+1），求m的值；
（3）若抛物线y=ax2+2（a-3）x+a+3+k上存在两个不同的点P、Q关于原点对称，求k的取值范围．
查看答案和解析>>
科目：czsx
来源：
题型：
已知△ABC的两边AB、AC的长是关于x的一元二次方程x2-（2k+3）x+k2+3k+2=0有两个实数根，第三边BC的长为5．
（1）求证：无论k为何值，关于x的一元二次方程x2-（2k+3）x+k2+3k+2=0都有两个不相等的实数根；
（2）当k为何值时，△ABC是直角三角形；
（3）当k为何值时，△ABC是等腰三角形，并求△ABC的周长．
查看答案和解析>>
科目：czsx
来源：
题型：
已知关于x的一元二次方程x2-2x-m=0．
（1）若方程有两个不实数根，求实数m的取值范围；
（2）在-3，-2，-1，0，1，2六个数中任取一个数作为m的取值，代入方程x2-2x-m=0，求使得方程有两个不相等的实数根的概率．
查看答案和解析>>
科目：czsx
来源：
题型：
（2013•海门市二模）已知关于x的一元二次方程x2+2（k-1）x+k2-1=0有两个不相等的实数根．
（1）求实数k的取值范围；
（2）0可能是方程的一个根吗？若是，请求出它的另一个根；若不是，请说明理由；
（3）若此方程的两个实数根的平方和为30，求实数k．
查看答案和解析>>
科目：czsx
来源：
题型：
已知关于x的一元二次方程x
2+2（k-1）x+k
2-1=0有两个不相等的实数根．则k
＜1
＜1
．
查看答案和解析>>
科目：czsx
来源：
题型：解答题
已知：关于x的一元二次方程ax2+2（a-3）x+a+3=0有两个实数根，且a为非负整数．
（1）求a的值；
（2）若抛物线y=ax2+2（a-3）x+a+3向下平移m（m＞0）个单位后过点（1，n）和点（2，2n+1），求m的值；
（3）若抛物线y=ax2+2（a-3）x+a+3+k上存在两个不同的点P、Q关于原点对称，求k的取值范围．
查看答案和解析>>
科目：czsx
来源：
题型：阅读理解
阅读材料：
若一元二次方程ax2+bx+c=0(a≠0)的两个实根为x1、x2，则两根与方程系数之间有如下关系：x1+x2= －，x1x2= 根据上述材料解决下列问题：
已知关于x的一元二次方程x2 = 2（1－m）x－m2 有两个实数根：x1，x2．
（1）求m的取值范围；
（2）设y =" x1" + x2，当y取得最小值时，求相应m的值，并求出最小值
查看答案和解析>>
科目：czsx
来源：2010-2011学年北京市石景山区九年级（上）期末数学试卷（解析版）
题型：解答题
已知：关于x的一元二次方程ax2+2（a-3）x+a+3=0有两个实数根，且a为非负整数．
（1）求a的值；
（2）若抛物线y=ax2+2（a-3）x+a+3向下平移m（m＞0）个单位后过点（1，n）和点（2，2n+1），求m的值；
（3）若抛物线y=ax2+2（a-3）x+a+3+k上存在两个不同的点P、Q关于原点对称，求k的取值范围．
查看答案和解析>>
科目：czsx
来源：2011-2012学年江苏省东台市九年级下学期学情调查（一）数学卷
题型：解答题
查看答案和解析>>
科目：czsx
来源：
题型：阅读理解
阅读材料：
若一元二次方程ax2+bx+c=0(a≠0)的两个实根为x1、x2，则两根与方程系数之间有如下关系：x1+x2= －，x1x2= 根据上述材料解决下列问题：
已知关于x的一元二次方程x2 = 2（1－m）x－m2 有两个实数根：x1，x2．
（1）求m的取值范围；
（2）设y = x1 + x2，当y取得最小值时，求相应m的值，并求出最小值
查看答案和解析>>
的一元二次方程
（m为实数）
的取值范围；
总过
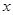的一元二次方程
（
为常数）
，
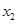为方程的两个实数根，且
，试求出方程的两个实数根和