
科目:czsx 来源: 题型:
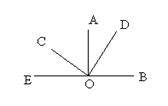
如图,已知AO⊥OB,CO⊥DO,∠BOC=![]() °,则∠AOD的度数为( )
°,则∠AOD的度数为( )
A、![]() °- 90° B、2
°- 90° B、2![]() °- 90° C、180°-
°- 90° C、180°-![]() ° D、2
° D、2![]() °- 180°
°- 180°
科目:czsx 来源: 题型:
 如图,已知抛物线y=-
如图,已知抛物线y=-| 4 | 9 |
科目:czsx 来源:2012届浙江省八年级上学期期中数学试卷(解析版) 题型:解答题
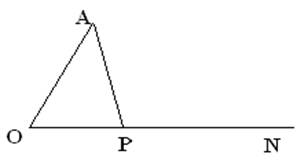
如图,已知AO=6,P是射线ON上一动点(即P点可在射线ON上运动),∠AON=60º,设OP=x,那么
(1)当x为 时,△AOP为等边三角形;
(2)当x为 时,△AOP为直角三角形;
(3)当x满足 条件时,△AOP为锐角三角形;
(4)当x满足 条件时,△AOP为钝角三角形。
科目:czsx 来源:2010-2011学年浙江省宁波东恩中学八年级上学期期中数学试卷(带解析) 题型:解答题
如图,已知AO=6,P是射线ON上一动点(即P点可在射线ON上运动),∠AON=60º,设OP=x,那么
(1)当x为 时,△AOP为等边三角形;
(2)当x为 时,△AOP为直角三角形;
(3)当x满足 条件时,△AOP为锐角三角形;
(4)当x满足 条件时,△AOP为钝角三角形。
科目:czsx 来源:2010-2011学年甘肃省靖远县七年级上学期期末数学试卷(带解析) 题型:解答题
如图,已知AO⊥OC,OB⊥OD,∠AOB =142°,求∠COD的度数。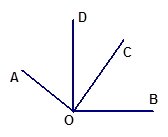
科目:czsx 来源: 题型:
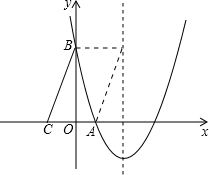 (-1,0),把△BOC向右平移2个单位长度后,一条直角边恰好在抛物线的对称轴上.
(-1,0),把△BOC向右平移2个单位长度后,一条直角边恰好在抛物线的对称轴上.科目:czsx 来源: 题型:
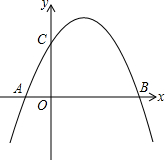 如图,已知抛物线y=-
如图,已知抛物线y=-| 2 | 3 |
科目:czsx 来源: 题型:
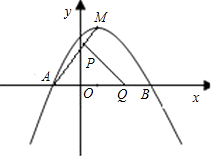 点运动,若P、Q同时出发,当其中的一点到达终点时,另一点也随之停止运动,设运动时间为t秒钟.
点运动,若P、Q同时出发,当其中的一点到达终点时,另一点也随之停止运动,设运动时间为t秒钟.科目:czsx 来源: 题型:
 如图,已知抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0)两点,且过点(-1,16),抛物线的顶点是点C,对称轴与x轴的交点为点D,原点为点O.在y轴的正半轴上有一动点N,使以A、O、N这三点为顶点的三角形与以C、A、D这三点为顶点的三角形相似.求:
如图,已知抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0)两点,且过点(-1,16),抛物线的顶点是点C,对称轴与x轴的交点为点D,原点为点O.在y轴的正半轴上有一动点N,使以A、O、N这三点为顶点的三角形与以C、A、D这三点为顶点的三角形相似.求: