
科目:gzsx 来源: 题型:
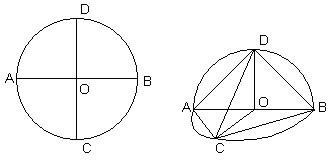
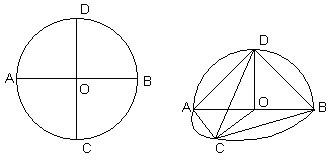 ⊙O半径为
⊙O半径为| 2 |
| ||
| 3 |
科目:gzsx 来源:2010年高三数学高考预测系列试卷:解答题(解析版) 题型:解答题
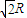 ,AB,CD是互相垂直的直径,沿AB将圆面折成大小为θ的二面角.
,AB,CD是互相垂直的直径,沿AB将圆面折成大小为θ的二面角.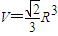 ?
?
科目:gzsx 来源:2010年广东省广州市番禺区仲元中学高三考前练笔数学试卷(理科)(解析版) 题型:解答题
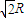 ,AB,CD是互相垂直的直径,沿AB将圆面折成大小为θ的二面角.
,AB,CD是互相垂直的直径,沿AB将圆面折成大小为θ的二面角.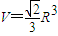 ?
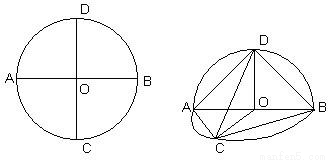
?
科目:gzsx 来源: 题型:解答题
 ⊙O半径为
⊙O半径为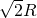 ,AB,CD是互相垂直的直径,沿AB将圆面折成大小为θ的二面角.
,AB,CD是互相垂直的直径,沿AB将圆面折成大小为θ的二面角.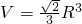 ?
?科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:解答题
科目:gzsx 来源: 题型:
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为线段AD1上的点,且满足
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为线段AD1上的点,且满足| D1P |
| PA |
科目:gzsx 来源: 题型:
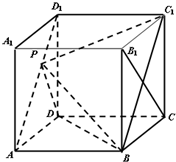 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为线段AD1上的点,且满足
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为线段AD1上的点,且满足| D1P |
| PA |
科目:gzsx 来源:2011年江苏省泰州市兴化市高三调研数学试卷(一)(解析版) 题型:解答题
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为线段AD1上的点,且满足
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为线段AD1上的点,且满足 .
.科目:gzsx 来源:2010-2011学年江苏省连云港市东海高级中学高三(下)3月月考数学试卷(实验班)(解析版) 题型:解答题
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为线段AD1上的点,且满足
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为线段AD1上的点,且满足 .
.科目:gzsx 来源:2010年广东省佛山市高三4月质量检测数学试卷2(理科)(解析版) 题型:解答题
 .
.
科目:gzsx 来源:不详 题型:解答题
| D1P |
| PA |

科目:gzsx 来源:2010年江苏省连云港市高考数学信息试卷(解析版) 题型:解答题
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为线段AD1上的点,且满足
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为线段AD1上的点,且满足 .
.科目:gzsx 来源:2014届江苏省高二上学期中考试数学试卷(解析版) 题型:解答题
(本小题满分15分)
如图,在半径为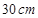 的
的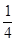 圆形(
圆形( 为圆心)铝皮上截取一块矩形材料
为圆心)铝皮上截取一块矩形材料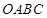 ,其中点
,其中点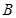 在圆上,点
在圆上,点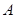 、
、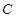 在两半径上,现将此矩形铝皮
在两半径上,现将此矩形铝皮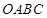 卷成一个以
卷成一个以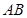 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长 ,圆柱的体积为
,圆柱的体积为
 .
.

(1)写出体积 关于
关于 的函数关系式,并指出定义域;
的函数关系式,并指出定义域;
(2)当 为何值时,才能使做出的圆柱形罐子体积
为何值时,才能使做出的圆柱形罐子体积 最大?最大体积是多少?
最大?最大体积是多少?
科目:gzsx 来源:浙江省衢州市2009-2010学年度第二学期高二第一次检测数学(理) 题型:解答题
(本小题满分15分)
如图,在三棱锥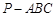 中,
中,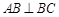 ,
,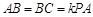 ,点
,点 分别是
分别是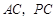 的中点,
的中点, 底面
底面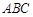 .
.
(1)求证: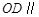 平面
平面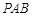 ;
;
(2)当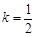 时,求直线
时,求直线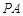 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)当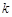 为何值时,
为何值时,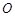 在平面
在平面 内的射影恰好为
内的射影恰好为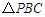 的重心.
的重心.

科目:gzsx 来源:2010-2011学年辽宁省高三第一次模拟考试数学理卷 题型:解答题
选修4—4:坐标系与参数方程
(本题满分l0分)
在直角坐标系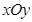 中,以O为极点,
中,以O为极点, 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为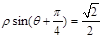 .圆O的参数方程为
.圆O的参数方程为 ,(
,(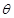 为参数,
为参数, )
)
(I)求圆心的一个极坐标;
(Ⅱ)当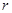 为何值时,圆O上的点到直线
为何值时,圆O上的点到直线 的最大距离为3.
的最大距离为3.
科目:gzsx 来源:广东省2012届高二下学期期末考试数学(理) 题型:解答题
(14分)在直角坐标系 中,以O为极点,
中,以O为极点, 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为 .圆O的参数方程为
.圆O的参数方程为 ,(
,( 为参数,
为参数, )
)
(1)求 圆心的极坐标;
圆心的极坐标;
(2)当 为何值时,圆O上的点到直线
为何值时,圆O上的点到直线 的最大距离为3.
的最大距离为3.
科目:gzsx 来源:2012-2013学年山东省高三高考模拟卷(二)文科数学试卷(解析版) 题型:解答题
如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使得平面ABEF 平面EFDC.
平面EFDC.
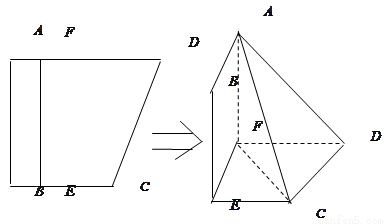
(Ⅰ) 当 ,是否在折叠后的AD上存在一点
,是否在折叠后的AD上存在一点 ,且
,且 ,使得CP∥平面ABEF?若存在,求出
,使得CP∥平面ABEF?若存在,求出 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(Ⅱ) 设BE=x,问当x为何值时,三棱锥A CDF的体积有最大值?并求出这个最大值.
CDF的体积有最大值?并求出这个最大值.
科目:gzsx 来源:2012届度湖北省师大一附中上学期高三期中检测理科数学试卷 题型:解答题
某城市计划在如图所示的空地 上竖一块长方形液晶广告屏幕
上竖一块长方形液晶广告屏幕 ,宣传该城市未来十年计划、目标等相关政策.已知四边形
,宣传该城市未来十年计划、目标等相关政策.已知四边形 是边长为30米的正方形,电源在点
是边长为30米的正方形,电源在点 处,点
处,点 到边
到边 的距离分别为9米,3米,且
的距离分别为9米,3米,且 ,线段
,线段 必过点
必过点 ,端点
,端点 分别在边
分别在边 上,设
上,设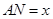 米,液晶广告屏幕
米,液晶广告屏幕 的面积为
的面积为 平方米.
平方米.
(Ⅰ)求 关于
关于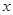 的函数关系式及其定义域;
的函数关系式及其定义域;
(Ⅱ)当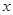 为何值时,液晶广告屏幕
为何值时,液晶广告屏幕 的面积
的面积 最小?
最小?

科目:gzsx 来源:2011届辽宁省东北育才学校高三第一次模拟考试数学理卷 题型:解答题
选修4—4:坐标系与参数方程
(本题满分l0分)
在直角坐标系 中,以O为极点,
中,以O为极点, 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为 .圆O的参数方程为
.圆O的参数方程为 ,(
,( 为参数,
为参数, )
)
(I)求圆心的一个极坐标;
(Ⅱ)当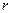 为何值时,圆O上的点到直线
为何值时,圆O上的点到直线 的最大距离为3.
的最大距离为3.