
科目:czsx 来源: 题型:
| ||
| 3 |
| 3 |

科目:czsx 来源:2011-2012年北京市九年级第一学期期中考试数学卷 题型:解答题
已知如图:二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,若AC=20,BC=15,∠ACB=90O,求:二次函数解析式。
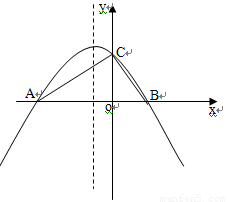
科目:czsx 来源:2011届北京市海淀区初三一模数学试题 题型:解答题
已知如图,二次函数y="ax2" +b x+c的图像过A、B、C三点
x+c的图像过A、B、C三点
观察图像写出A、B、C三点的坐标
求出二次函数的解析式
科目:czsx 来源: 题型:解答题
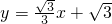 对称.
对称.
科目:czsx 来源:2012年湖北省天门市中考数学模拟试卷(一)(解析版) 题型:解答题
 对称.
对称.
科目:czsx 来源:2010-2011学年北京市海淀区初三一模数学试题 题型:解答题
已知如图,二次函数y=ax2 +bx+c的图像过A、B、C三点

观察图像写出A、B、C三点的坐标
求出二次函数的解析式
科目:czsx 来源:2011-2012学年北京市第六十二中学九年级第一学期期中考试数学卷 题型:解答题
已知如图:二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,若AC=20,BC=15,∠ACB=90O,求:二次函数解析式。
科目:czsx 来源:2012年人教版初中数学九年级下26.1二次函数及其图像练习卷(解析版) 题型:解答题
已知如图,二次函数y=ax2 +bx+c的图像过A、B、C三点
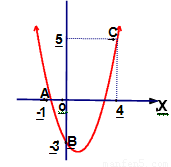
(1)观察图像写出A、B、C三点的坐标
(2)求出二次函数的解析式
科目:czsx 来源:2012届江苏省无锡市新区九年级下学期期中考试数学卷(带解析) 题型:解答题
已知如图,二次函数
 图象的顶点为
图象的顶点为 ,与
,与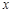 轴交于
轴交于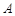 、
、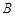 两点(
两点(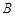 在
在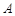 点右侧),点
点右侧),点 、
、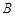 关于直线
关于直线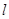 :
: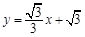 对称.
对称.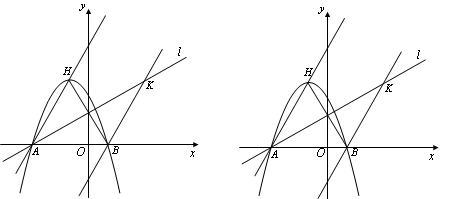
(1)求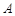 、
、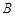 两点坐标,并证明点
两点坐标,并证明点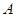 在直线
在直线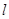 上;
上;
(2)求二次函数解析式;
(3)过点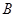 作直线
作直线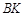 ∥
∥ 交直线
交直线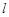 于
于 点,
点,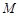 、
、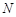 分别为直线
分别为直线 和直线
和直线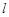 上的两个动点,连接
上的两个动点,连接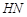 、
、 、
、 ,求
,求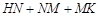 和的最小值.
和的最小值.
科目:czsx 来源: 题型:
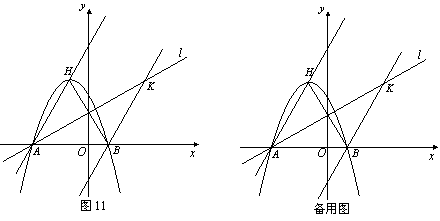
已知,如图11,二次函数![]()
![]() 图象的顶点为
图象的顶点为![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 点右侧),点
点右侧),点![]() 、
、![]() 关于直线
关于直线![]() :
:![]() 对称.
对称.
(1)求![]() 、
、![]() 两点坐标,并证明点
两点坐标,并证明点![]() 在直线
在直线![]() 上;
上;
(2)求二次函数解析式;
(3)过点![]() 作直线
作直线![]() ∥
∥![]() 交直线
交直线![]() 于
于![]() 点,
点,![]() 、
、![]() 分别为直线
分别为直线![]() 和直线
和直线![]() 上的两个动点,连接
上的两个动点,连接![]() 、
、![]() 、
、![]() ,求
,求![]() 和的最小值.
和的最小值.
 |
科目:czsx 来源: 题型:
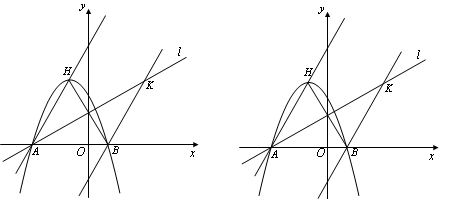
已知如图,二次函数![]()
![]() 图象的顶点为
图象的顶点为![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 点右侧),点
点右侧),点![]() 、
、![]() 关于直线
关于直线![]() :
:![]() 对称.
对称.
(1)求![]() 、
、![]() 两点坐标,并证明点
两点坐标,并证明点![]() 在直线
在直线![]() 上;
上;
(2)求二次函数解析式;
(3)过点![]() 作直线
作直线![]() ∥
∥![]() 交直线
交直线![]() 于
于![]() 点,
点,![]() 、
、![]() 分别为直线
分别为直线![]() 和直线
和直线![]() 上的两个动点,连接
上的两个动点,连接![]() 、
、![]() 、
、![]() ,求
,求![]() 和的最小值.
和的最小值.
【解析】(1)根据一元二次方程求得A点坐标,代入直线求证,(2)通过点H、B关于直线L对称,求得H的坐标,从而解出二次函数的解析式,(3)先求出HN+MN的最小值是MB, 再求出BM+MK的最小值是BQ,即![]() 和的最小值
和的最小值
科目:czsx 来源:2011-2012学年江苏省无锡市新区九年级下学期期中考试数学卷(解析版) 题型:解答题
已知如图,二次函数
 图象的顶点为
图象的顶点为 ,与
,与 轴交于
轴交于 、
、 两点(
两点( 在
在 点右侧),点
点右侧),点 、
、 关于直线
关于直线 :
: 对称.
对称.

(1)求 、
、 两点坐标,并证明点
两点坐标,并证明点 在直线
在直线 上;
上;
(2)求二次函数解析式;
(3)过点 作直线
作直线 ∥
∥ 交直线
交直线 于
于 点,
点, 、
、 分别为直线
分别为直线 和直线
和直线 上的两个动点,连接
上的两个动点,连接 、
、 、
、 ,求
,求 和的最小值.
和的最小值.
【解析】(1)根据一元二次方程求得A点坐标,代入直线求证,(2)通过点H、B关于直线L对称,求得H的坐标,从而解出二次函数的解析式,(3)先求出HN+MN的最小值是MB, 再求出BM+MK的最小值是BQ,即 和的最小值
和的最小值
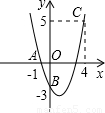
科目:czsx 来源:《20.1 二次函数》2010年同步试卷(解析版) 题型:解答题
科目:czsx 来源: 题型:
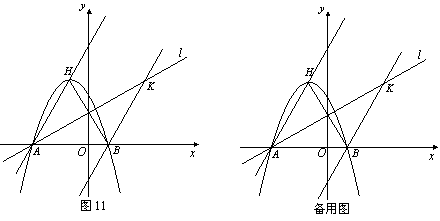
已知,如图11,二次函数![]()
![]() 图象的顶点为
图象的顶点为![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 点右侧),点
点右侧),点![]() 、
、![]() 关于直线
关于直线![]() :
:![]() 对称.
对称.
(1)求![]() 、
、![]() 两点坐标,并证明点
两点坐标,并证明点![]() 在直线
在直线![]() 上;
上;
(2)求二次函数解析式;
(3)过点![]() 作直线
作直线![]() ∥
∥![]() 交直线
交直线![]() 于
于![]() 点,
点,![]() 、
、![]() 分别为直线
分别为直线![]() 和直线
和直线![]() 上的两个动点,连接
上的两个动点,连接![]() 、
、![]() 、
、![]() ,求
,求![]() 和的最小值.
和的最小值.
 |