如图在直角坐标系中已知O(0,0)A(2,0)B(0,4)答案解析
科目:czsx
来源:
题型:
如图,在直角坐标系中,已知点A(-3,0),B(0,4), 对  连续作旋转变换,依次得带三角形 ①,②,③,④,…,三角形⑩的直角顶点的坐标为__________
连续作旋转变换,依次得带三角形 ①,②,③,④,…,三角形⑩的直角顶点的坐标为__________

查看答案和解析>>
科目:czsx
来源:
题型:
如图,在直角坐标系中,已知点A(-3,0),B(0,4),对 连续作旋转变换,依次得带三角形①,②,③,④,…,则三角形⑩的直角顶点的坐标为__________
连续作旋转变换,依次得带三角形①,②,③,④,…,则三角形⑩的直角顶点的坐标为__________

查看答案和解析>>
科目:czsx
来源:
题型:
如图,在直角坐标系中,已知点A(-3,0),B(0,4), 对  连续作旋转变换,依次得带三角形 ①,②,③,④,…,三角形⑩的直角顶点的坐标为__________
连续作旋转变换,依次得带三角形 ①,②,③,④,…,三角形⑩的直角顶点的坐标为__________

查看答案和解析>>
科目:czsx
来源:
题型:
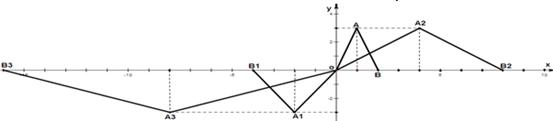
20、如图 在直角坐标系中第一次将△OAB变换成△OA
1B
1,第二次又变换△OA
2B
2第三次变换成△OA
3B
3,已知:A(1,3)A
1(-2,-3)A
2(4,3)A
3(-8,-3);B(2,0)B
1(-4,0)B
2(8,0)B
3(-16,0)
(1)观察每次变化前后的三角形有何变化,找出其中的规律,按此变化规律变换成△0A
4B
4则点A
4的坐标为
(16,3)
,点B
4的坐标为
(32,0)
.
(2)若按第(1题)中找到的规律将△OAB进行了n次变换,得到的△OAnBn推测点An坐标为
((-1)n•2n,(-1)n•3)
,点Bn坐标为
((-1)n•2n+1,0)
.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图 在直角坐标系中第一次将△OAB变换成△OA1B1,第二次又变换△OA2B2第三次变换成△OA3B3,已知:A(1,3)A1(-2,-3)A2(4,3)A3(-8,-3);B(2,0)B1(-4,0)B2(8,0)B3(-16,0)
(1)观察每次变化前后的三角形有何变化,找出其中的规律,按此变化规律变换成△0A4B4则点A4的坐标为______,点B4的坐标为______.
(2)若按第(1题)中找到的规律将△OAB进行了n次变换,得到的△OAnBn推测点An坐标为______,点Bn坐标为______.
查看答案和解析>>
科目:czsx
来源:
题型:
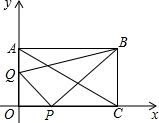
己知,如图在直角坐标系中,矩形OABC的对角线AC所在直线的解析式为y=-
+1.
(1)求线段AC的长和∠ACO的度数;
(2)动点P从点C开始在线段CO上以每秒
个单位长度的速度向点O移动,动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,(P、Q两点同时开始移动)设P、Q移动的时间为t秒.
①设△BPQ的面积为S,求S与t之间的函数关系式,并求出当t为何值时,S有最小值;
②是否存在这样的时刻t,使得△OPQ与△BCP相似,并说明理由;
(3)在坐标平面内存在这样的点M,使得△MAC为等腰三角形且底角为30°,写出所有符合要求的点M的坐标.
查看答案和解析>>
科目:czsx
来源:2009年福建省福州市平潭县城关中学数学模拟考试卷(解析版)
题型:解答题
己知,如图在直角坐标系中,矩形OABC的对角线AC所在直线的解析式为y=-
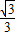
+1.
(1)求线段AC的长和∠ACO的度数;
(2)动点P从点C开始在线段CO上以每秒
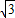
个单位长度的速度向点O移动,动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,(P、Q两点同时开始移动)设P、Q移动的时间为t秒.
①设△BPQ的面积为S,求S与t之间的函数关系式,并求出当t为何值时,S有最小值;
②是否存在这样的时刻t,使得△OPQ与△BCP相似,并说明理由;
(3)在坐标平面内存在这样的点M,使得△MAC为等腰三角形且底角为30°,写出所有符合要求的点M的坐标.
查看答案和解析>>
科目:czsx
来源:湖北省模拟题
题型:解答题
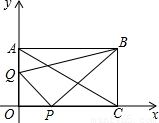
己知,如图在直角坐标系中,矩形OABC的对角线AC所在直线的解析式为y= -
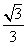
x+1 。
(1)求线段AC的长和∠ACO的度数。
(2)动点P从点C开始在线段CO上以每秒
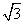
个单位长度的速度向点O移动,动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,(P、Q两点同时开始移动)设P、Q移动的时间为t秒。
①设△BPQ的面积为S,求S与t之间的函数关系式,并求出当t为何值时,S有最小值。
②是否存在这样的时刻t,使得△OPQ与△BCP相似,并说明理由?
(3)在坐标平面内存在这样的点M,使得△MAC 为等腰三角形且底角为30°,写出所有符合要求的点M的坐标。
查看答案和解析>>
科目:czsx
来源:
题型:解答题
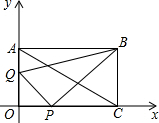 己知,如图在直角坐标系中,矩形OABC的对角线AC所在直线的解析式为y=-
己知,如图在直角坐标系中,矩形OABC的对角线AC所在直线的解析式为y=- +1.
+1.
(1)求线段AC的长和∠ACO的度数;
(2)动点P从点C开始在线段CO上以每秒 个单位长度的速度向点O移动,动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,(P、Q两点同时开始移动)设P、Q移动的时间为t秒.
个单位长度的速度向点O移动,动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,(P、Q两点同时开始移动)设P、Q移动的时间为t秒.
①设△BPQ的面积为S,求S与t之间的函数关系式,并求出当t为何值时,S有最小值;
②是否存在这样的时刻t,使得△OPQ与△BCP相似,并说明理由;
(3)在坐标平面内存在这样的点M,使得△MAC为等腰三角形且底角为30°,写出所有符合要求的点M的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
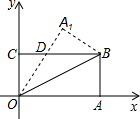
如图在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A
1处,OB=8,OC=4,则△BDO的面积为
10
10
.
查看答案和解析>>
科目:czsx
来源:
题型:
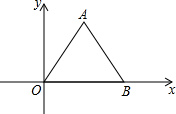
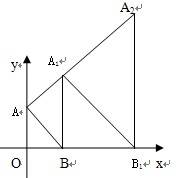
如图在直角坐标系中,△AOB是等边三角形,若B点的坐标是(2,0),则A点的坐标是( )
| | | |
查看答案和解析>>
科目:czsx
来源:
题型:
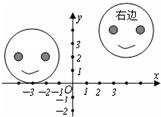
24、(北师大版)如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是(-4,2)、(-2,2),右图中左眼的坐标是(3,4),则右图案中右眼的坐标是
(5,4)
.
查看答案和解析>>
科目:czsx
来源:
题型:
如图在直角坐标系中,二次函数y=x
2-4x+k的顶点是C,与x轴相交于A,B两点(A在B的左边).
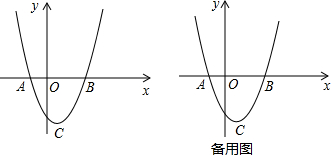
(1)若点B的横坐标x
B满足5<x
B<6,求k的取值范围;
(2)若tan∠ACB=
,求k的值;
(3)当k=0时,点D,E同时从点B出发,分别向左、向右在抛物线上移动,点D,E在x轴上的正投影分别为M,N,设BM=m(m<OB),BN=n,当m,n满足怎样的等量关系时,△ODE的内心在x轴上?
查看答案和解析>>
科目:czsx
来源:
题型:
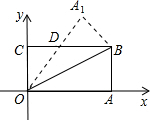
如图在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A
1处,OA=8,OC=4,则△BDO的面积为
,点A
1的坐标为
.
查看答案和解析>>
科目:czsx
来源:
题型:
如图在直角坐标系中,A(-2,0),B(8,0),以AB为直径的半圆P与y轴交于点M,以AB为

一边作正方形ABCD交y轴于E.
(1)写出AB边的长;
(2)连接CM,试说明直线CM是否与⊙P相切,说理理由;
(3)在x轴的正半轴上是否存在一点N,使得⊙N与⊙P、直线CP都相切?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图:在直角坐标系中,线段OA=6cm,OA与y轴的夹角为30º.将线段OA绕原点按逆时针方向旋转到

轴的负半轴上,得到线段OB.
【小题1】点A经过的路径是一条____(填“线段”或“弧”),并求出此“路径”的长度;(6分)
【小题2】求线段OA转到OB位置时,OA所“扫描” 过的图形的面积.(4分)

查看答案和解析>>
科目:czsx
来源:2012届福建建宁九年级学业质量检测考试数学试卷(带解析)
题型:解答题
如图:在直角坐标系中,线段OA=6cm,OA与y轴的夹角为30º.将线段OA绕原点按逆时针方向旋转到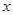 轴的负半轴上,得到线段OB.
轴的负半轴上,得到线段OB.
【小题1】点A经过的路径是一条____(填“线段”或“弧”),并求出此“路径”的长度;(6分)
【小题2】求线段OA转到OB位置时,OA所“扫描” 过的图形的面积.(4分)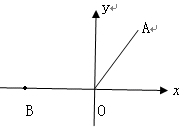
查看答案和解析>>
科目:czsx
来源:2011-2012学年福建省南安市初二下学期期末考试数学卷(解析版)
题型:解答题
如图, 在直角坐标系中,矩形ABCD的边BC在X轴上,点B、D的坐标分别为B(1,0),D(3,3).

(1)直接写出点C的坐标;
(2)若反比例函数 的图象经过直线AC上的点E,且点E的坐标为(2,m),求
的图象经过直线AC上的点E,且点E的坐标为(2,m),求 的值及反比例函数的解析式;
的值及反比例函数的解析式;
(3)若(2)中的反比例函数的图象与CD相交于点F,连接 EF,在线段AB上(端点除外)找一点P,使得:S△PEF=S△CEF,并求出点P的坐标.
查看答案和解析>>
科目:czsx
来源:2011-2012学年云南省九年级上学期期末考试数学卷
题型:填空题
如图,在直角坐标系中,右边的蝴蝶是由左边的蝴蝶飞过去以后得到的,左图案中左右翅尖的坐标分别是(-4,2)、(-2,2),右图案中左翅尖的坐标是(3,4),则右图案中右翅尖的坐标是
。

查看答案和解析>>

![]() 连续作旋转变换,依次得带三角形 ①,②,③,④,…,三角形⑩的直角顶点的坐标为__________
连续作旋转变换,依次得带三角形 ①,②,③,④,…,三角形⑩的直角顶点的坐标为__________
![]() 连续作旋转变换,依次得带三角形①,②,③,④,…,则三角形⑩的直角顶点的坐标为__________
连续作旋转变换,依次得带三角形①,②,③,④,…,则三角形⑩的直角顶点的坐标为__________
![]() 连续作旋转变换,依次得带三角形 ①,②,③,④,…,三角形⑩的直角顶点的坐标为__________
连续作旋转变换,依次得带三角形 ①,②,③,④,…,三角形⑩的直角顶点的坐标为__________


![]() ,
,![]() ) B(
) B(![]() ,
,![]() ) C.(
) C.(![]() ,
, ![]() ) D.(
) D.(![]() ,
,![]() )
) 己知,如图在直角坐标系中,矩形OABC的对角线AC所在直线的解析式为y=-
己知,如图在直角坐标系中,矩形OABC的对角线AC所在直线的解析式为y=-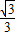 +1.
+1.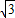 个单位长度的速度向点O移动,动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,(P、Q两点同时开始移动)设P、Q移动的时间为t秒.
个单位长度的速度向点O移动,动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,(P、Q两点同时开始移动)设P、Q移动的时间为t秒.
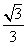 x+1 。
x+1 。 个单位长度的速度向点O移动,动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,(P、Q两点同时开始移动)设P、Q移动的时间为t秒。
个单位长度的速度向点O移动,动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,(P、Q两点同时开始移动)设P、Q移动的时间为t秒。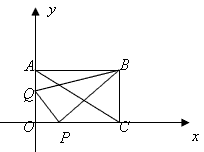
 己知,如图在直角坐标系中,矩形OABC的对角线AC所在直线的解析式为y=-
己知,如图在直角坐标系中,矩形OABC的对角线AC所在直线的解析式为y=- +1.
+1. 个单位长度的速度向点O移动,动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,(P、Q两点同时开始移动)设P、Q移动的时间为t秒.
个单位长度的速度向点O移动,动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,(P、Q两点同时开始移动)设P、Q移动的时间为t秒. 24、(北师大版)如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是(-4,2)、(-2,2),右图中左眼的坐标是(3,4),则右图案中右眼的坐标是
24、(北师大版)如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是(-4,2)、(-2,2),右图中左眼的坐标是(3,4),则右图案中右眼的坐标是
 一边作正方形ABCD交y轴于E.
一边作正方形ABCD交y轴于E. 轴的负半轴上,得到线段OB.
轴的负半轴上,得到线段OB.
 轴的负半轴上,得到线段OB.
轴的负半轴上,得到线段OB.

 的图象经过直线AC上的点E,且点E的坐标为(2,m),求
的图象经过直线AC上的点E,且点E的坐标为(2,m),求 的值及反比例函数的解析式;
的值及反比例函数的解析式;