科目：gzsx 来源：2012-2013学年福建省高三上学期期中文科数学试卷（解析版） 题型：解答题
（本题满分12分）
已知函数f(x)=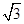
cos2x+sinxcosx
.
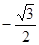（1）求函数f（x）的单调递增区间；
(2)若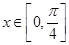
，求函数f（x）的取值范围；
科目：gzsx 来源： 题型：
已知函数f(x)=
cos2x+sinxcosx
.
（1）求函数f（x）的单调递增区间；
（2）若
，求函数f（x）的取值范围；
（3）函数f（x）的图象经过怎样的平移可使其对应的函数成为奇函数？
科目：gzsx 来源：江西省师大附中、鹰潭一中2012届高三4月联考数学理科试题 题型：044
已知函数f(x)＝
sinxcosx－cos2x－
，x∈R
(1)求函数f(x)的最大值和最小正周期；
(2)设△ABC的内角A，B，C的对边分别a，b，c且c＝3，f(C)＝0，若sin(A＋C)＝2sinA，求a，b的值．
科目：gzsx 来源：江西省师大附中、鹰潭一中2012届高三4月联考数学文科试题 题型：044
已知函数f(x)＝
sinxcosx－cos2x－
，x∈R
(1)求函数f(x)的最大值和最小正周期；
(2)设△ABC的内角A，B，C的对边分别a，b，c且c＝3，f(C)＝0，若sin(A＋C)＝2sinA，求a，b的值．
科目：gzsx 来源：山东省淄博市2010届高三上学期期末考试理科数学试卷 题型：044
已知函数f(x)＝sinxcosx＋
cos2x．
(Ⅰ)求f(x)的最小正周期；
(Ⅱ)求f(x)在区间
上的最大值和最小值．
科目：gzsx 来源：上海市十校2012届高三第二次联考数学文科试题 题型：044
已知函数f(x)＝
sinxcosx－cos2x＋
(x∈R)．
(1)求函数f(x)的最小正周期；
(2)求函数f(x)在区间
上的函数值的取值范围．
科目：gzsx 来源：山东省德州市2012届高三第一次模拟考试数学理科试题 题型：044
已知函数f(x)＝
sinxcosx－cos2x＋
(x∈R)
(Ⅰ)求函数f(x)的最小正周期及在区间
上的值域；
(Ⅱ)在△ABC中，角A、B、C所对的边分别是a、b、c，又
b＝2，△ABC的面积等于3，求边长a的值．
科目：gzsx 来源：山东省淄博市2010届高三上学期期末考试文科数学试卷 题型：044
已知函数f(x)＝sinxcosx＋
cos2x．
(Ⅰ)求f(x)的最小正周期；
(Ⅱ)求f(x)在区间
上的最大值和最小值．
科目：gzsx 来源：广东省汕头市2012届高三毕业班教学质量检测数学理科试题 题型：044
已知函数f(x)＝
sinxcosx＝cos2x－
，x∈R．
(Ⅰ)求函数f(x)的最小值和最小正周期；
(Ⅱ)已知△ABC内角A、B、C的对边分别为a、b、c，且c＝3，f(C)＝0，若向量
＝(1，sinA)与n＝(2，sinB)共线，求a、b的值．
科目：gzsx 来源：山东省济钢高中2012届高三5月高考冲刺数学文科试题 题型：044
已知函数f(x)＝sinxcosx＋cos2x－
(x∈R)．
(Ⅰ)求函数f(x)的最小正周期；
(Ⅱ)求函数f(x)在区间[0，
]上的最大值与最小值．
科目：gzsx 来源：福建省四地六校2012届高三第一次联考数学文科试题 题型：044
已知函数f(x)＝
sinxcosx－cos2x－
，x∈R．
(Ⅰ)求函数f(x)的最小值和最小正周期；
(Ⅱ)已知△ABC内角A、B、C的对边分别为a、b、c，且c＝3，f(c)＝0，若向量
＝(1，sinA)与
＝(2，sinB)共线，求a、b的值．
科目：gzsx 来源：山东省德州市2012届高三第一次模拟考试数学文科试题 题型：044
已知函数f(x)＝
sinxcosx－cos2x＋
(x∈R)
(Ⅰ)求函数f(x)的最小正周期及在区间
上的值域；
(Ⅱ)在△ABC中，角A、B、C所对的边分别是a、b、c，又
面积S△ABC＝3，求边长a的值．
科目：gzsx 来源： 题型：
| 3 |
| 10 |
| 13 |
| π |
| 4 |
| π |
| 2 |
科目：gzsx 来源： 题型：
| 3 |
科目：gzsx 来源： 题型：
| x |
| 2 |
| x |
| 2 |
科目：gzsx 来源： 题型：
| 3 |
| ||
| 2 |
| π |
| 2 |
| 1 |
| 2 |
| BC |
| AB |
科目：gzsx 来源： 题型：
| 3 |
| ||
| 2 |
| π |
| 2 |
| 1 |
| 2 |
| BC |
| AB |
科目：gzsx 来源： 题型：
| π |
| 2 |
| π |
| 8 |
| 2 |
| π |
| 4 |
| 5π |
| 8 |