
科目:czsx 来源: 题型:
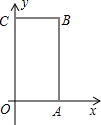 如图矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).
如图矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).科目:czsx 来源: 题型:
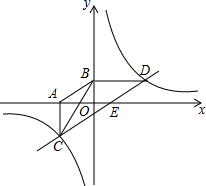 如图,已知点D(6,1)是反比例函数y=
如图,已知点D(6,1)是反比例函数y=| k | x |
科目:czsx 来源: 题型:
 如图,在Rt△OAB中,∠A=90°,∠ABO=30°,OB=
如图,在Rt△OAB中,∠A=90°,∠ABO=30°,OB=8
| ||
| 3 |
科目:czsx 来源: 题型:
 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+3的顶点为M(2,-1),交x轴与A、B两点,交y轴于点C,其中点B的坐标为(3,0).
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+3的顶点为M(2,-1),交x轴与A、B两点,交y轴于点C,其中点B的坐标为(3,0).科目:czsx 来源: 题型:
| 16 | 3 |
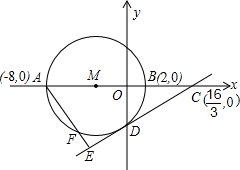 O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.
O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.科目:czsx 来源: 题型:
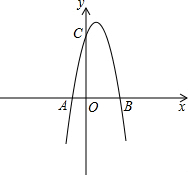 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8),
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8),科目:czsx 来源: 题型:
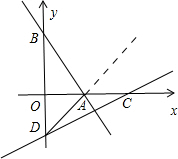 已知:如图,直线y=-
已知:如图,直线y=-| 3 |
| 3 |
科目:czsx 来源: 题型:
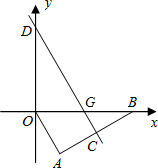
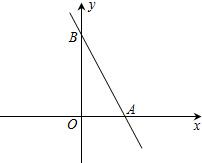 如图,直线AB分别与x轴、y轴相交于点A和点B,如果A(2,0),B(0,4)线段CD两端点在坐标轴上滑动(C点在y轴上,D点在x轴上),且CD=AB.
如图,直线AB分别与x轴、y轴相交于点A和点B,如果A(2,0),B(0,4)线段CD两端点在坐标轴上滑动(C点在y轴上,D点在x轴上),且CD=AB.科目:czsx 来源: 题型:
 :y=kx+10k交于点E,且E点的纵坐标为-2,
:y=kx+10k交于点E,且E点的纵坐标为-2,| 2 |
科目:czsx 来源: 题型:
| 5 |
| 5 |
| NQ |
| PQ |
| 2 |
| 3 |

科目:czsx 来源: 题型:
| 1 | 2 |
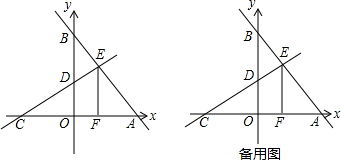
科目:czsx 来源: 题型:
 两点,交y轴于点C,其中点B的坐标为(3,0).
两点,交y轴于点C,其中点B的坐标为(3,0).科目:czsx 来源: 题型:
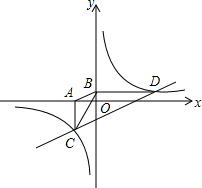 (2013•湖北模拟)如图,已知双曲线y=
(2013•湖北模拟)如图,已知双曲线y=| k | x |
科目:czsx 来源: 题型:
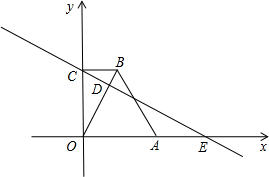
 (2013•莒南县二模)已知直线y=2x+2与x轴、y轴交于A、B两点,过点C(2,0)作直线AB的垂线,垂足为D.
(2013•莒南县二模)已知直线y=2x+2与x轴、y轴交于A、B两点,过点C(2,0)作直线AB的垂线,垂足为D.科目:czsx 来源: 题型:
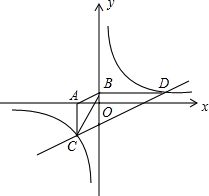 (2012•济南)如图,已知双曲线y=
(2012•济南)如图,已知双曲线y=| k | x |
科目:czsx 来源: 题型:
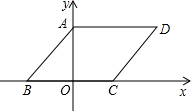 如图,▱ABCD在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.
如图,▱ABCD在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.科目:czsx 来源: 题型:
| 5 |
 分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.
分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.科目:czsx 来源: 题型:
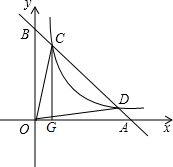 如图,已知C、D是双曲线y=
如图,已知C、D是双曲线y=| m |
| x |
| m |
| y1 |
| 10 |
| x1 |
| y1 |
| y2 |
| x2 |
| 1 |
| 3 |
科目:czsx 来源: 题型:
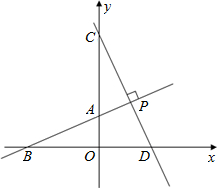 OB),点C在y轴上,且OA:AC=2:5,直线CD垂直于直线AB于点P,交x轴于点D.
OB),点C在y轴上,且OA:AC=2:5,直线CD垂直于直线AB于点P,交x轴于点D.科目:czsx 来源: 题型:
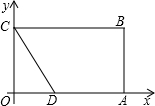 如图,在矩形OABC中,OA=8,OC=4,OA、OC分别在x,y轴上,点D在OA上,且CD=AD,
如图,在矩形OABC中,OA=8,OC=4,OA、OC分别在x,y轴上,点D在OA上,且CD=AD,