如图,已知抛物线y=-1/2x2+(5-√m2)答案解析
科目:czsx
来源:2007中考夺标冲刺模拟题(新课标)(十)、数学
题型:059
如图,已知抛物线y=2x2-4x+m与x轴交于不同的两点A、B,其顶点是C,点D是抛物线的对称轴与x轴的交点.

(1)求实数m的取值范围;
(2)求顶点C的坐标和线段AB的长度(用含有m的式子表示);
(3)若直线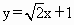 分别交x轴、y轴于点E、F,问△BDC与△EOF是否有可能全等,如果可能,请证明;如果不可能,请说明理由.
分别交x轴、y轴于点E、F,问△BDC与△EOF是否有可能全等,如果可能,请证明;如果不可能,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
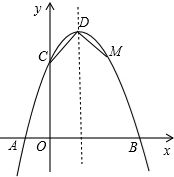
如图,已知抛物线与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
(3)点M是抛物线上一点,以B,C,D,M为顶点的四边形是直角梯形,试求出点M的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知抛物线
c1:y=-x2+bx+c与x轴交于点A、B(点A在B的左侧),与y轴交于点C,抛物线c
2与抛物线c
1关于y轴对称,点A、B的对称点分别是E、D,连接CD、CB,设AD=m.
(1)抛物线c
2可以看成抛物线c
1向右平移
m
m
个单位得到.
(2)若m=2,求b的值.
(3)将△CDB沿直线BC折叠,点D的对应点为G,且四边形CDBG是平行四边形,
①△CDB为
等边
等边
三角形(按边分);
②若点G恰好落在抛物线c
2上,求m的值.
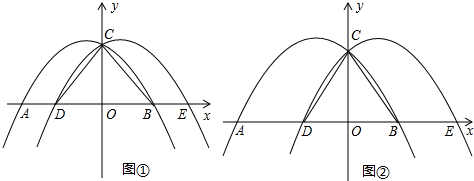
查看答案和解析>>
科目:czsx
来源:
题型:
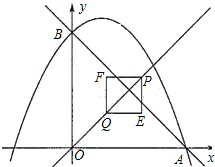
如图,已知抛物线y=-
x
2+x+4交x轴的正半轴于点A,交y轴于点B.
(1)求A、B两点的坐标,并求直线AB的解析式;
(2)设P(x,y)(x>0)是直线y=x上的一点,Q是OP的中点(O是原点),以PQ为对角线作正方形PEQF,若正方形PEQF与直线AB有公共点,求x的取值范围;
(3)在(2)的条件下,记正方形PEQF与△OAB公共部分的面积为S,求S关于x的函数解析式,并探究S的最大值.
查看答案和解析>>
科目:czsx
来源:
题型:
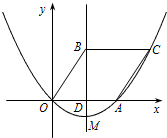
(2008•海口一模)如图,已知抛物线经过原点O和点A,点B(2,3)是该抛物线对称轴上一点,过点B作BC∥x轴交抛物线于点C,连接BO、CA,若四边形OACB是平行四边形.
(1)①直接写出A、C两点的坐标;
②求这条抛物线的函数关系式;
(2)设该抛物线的顶点为M,试在线段AC上找出这样的点P,使得△PBM是以BM为底边的等
腰三角形,并求出此时点P的坐标;
(3)经过点M的直线把▱OACB的面积分为1:3两部分,求这条直线的函数关系式.
查看答案和解析>>
科目:czsx
来源:
题型:

11、如图,已知抛物线y=x
2,把该抛物线向上平移,使平移后的抛物线经过点A(1,3),那么平移后的抛物线的表达式是
y=x2+2
.
查看答案和解析>>
科目:czsx
来源:
题型:

(2013•桐乡市一模)如图,已知抛物线y=ax
2+bx+c(a>0)的顶点坐标为(2,-3),将此抛物线在x轴下方的部分沿x轴往上翻折,得到一个新的函数图象(即图中的实线型图象).若|ax
2+bx+c|=k(k≠0)时,对应的x的值是两个不相等的实数,则常数k的取值范围是
k>3
k>3
.
查看答案和解析>>
科目:czsx
来源:
题型:
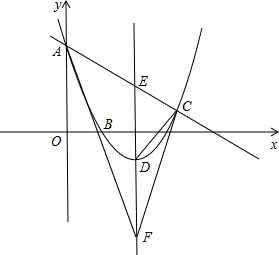
如图,已知抛物线过点A(0,6),B(2,0),C(7,
).
(1)求抛物线的解析式;
(2)若D是抛物线的顶点,E是抛物线的对称轴与直线AC的交点,F与E关于D对称,求证:∠CFE=∠AFE;
(3)在y轴上是否存在这样的点P,使△AFP与△FDC相似?若有请求出所有符和条件的点P的坐标;若没有,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
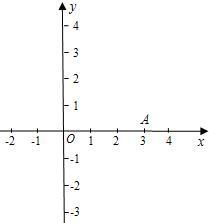
如图,已知抛物线y=-x
2+mx+3与x轴的一个交点A(3,0).
(1)你一定能分别求出这条抛物线与x轴的另一个交点B及与y轴的交点C的坐标,试试看;
(2)设抛物线的顶点为D,请在图中画出抛物线的草图.若点E(-2,n)在直线BC上,试判断E点是否在经过D点的反比例函数的图象上,把你的判断过程写出来;
(3)请设法求出tan∠DAC的值.
查看答案和解析>>
科目:czsx
来源:
题型:

(2011•梅州)如图,已知抛物线y=x
2-4x+3与x 轴交于两点A、B,其顶点为C.
(1)对于任意实数m,点M(m,-2)是否在该抛物线上?请说明理由;
(2)求证:△ABC是等腰直角三角形;
(3)已知点D在x轴上,那么在抛物线上是否存在点P,使得以B、C、D、P为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
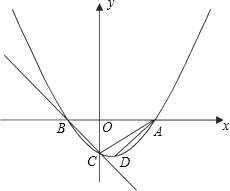
如图,已知抛物线
y=x2-x-1与x轴相交于点A、B,与y轴相交于C.
(1)求点A、B、C的坐标及直线BC的解析式;
(2)设抛物线的顶点为点D,求△ACD的面积S
(3)在直线BC上是否存在一点P,使△ACP是以AC为一腰的等腰三角形?若存在,求点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
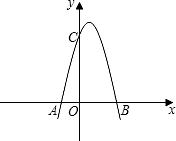
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴平移,使抛物线与线段EF总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知抛物线经过点B(-2,3),原点O和x轴上另一点A,它的对称轴与x轴交于点C
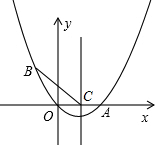
(2,0).
(1)求此抛物线的函数关系式;
(2)连接CB,在抛物线的对称轴上找一点E,使得CB=CE,求点E的坐标;
(3)在(2)的条件下,连接BE,设BE的中点为G,在抛物线的对称轴上是否存在点P,使得△PBG的周长最小?若存在,求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,已知抛物线y=ax
2+c交x轴于点A(-1,0)和点B,交y轴于点C(0,-1).
(1)求此抛物线的解析式.
(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积.
查看答案和解析>>
科目:czsx
来源:
题型:
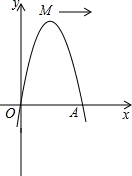
如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),
(1)求该抛物线的解析式;
(2)现将它向右平移m(m>0)个单位,所得抛物线与x轴交于C、D两点,与原抛物线交于点P,△CDP的面积为S,求S关于m的关系式;
(3)当m=2时,点Q为平移后的抛物线的一动点,是否存在这样的⊙Q,使得⊙Q与两坐标轴都相切?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
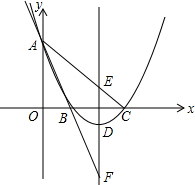
如图,已知抛物线过点A(0,6),B(2,0),C(6,0),直线AB交抛物线的对称轴于点F,直线AC交抛物线对称轴于点E.
(1)求抛物线的解析式;
(2)求证:点E与点F关于顶点D对称;
(3)在y轴上是否存在这样的点P,使△AFP与△FDC相似?若有,请求出所有合条件的点P的坐标;若没有,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

(2013•和平区二模)如图,已知抛物线y=ax
2+bx-2经过点A(2,3),B(6,1).
(Ⅰ)求此抛物线的解析式,Ⅰ把解析式化为顶点式;
(Ⅱ)点P是抛物线对称轴上的动点,当AP⊥CP时,求点P的坐标;
(Ⅲ)设直线BC与x轴交于点D,点H是抛物线与x轴的一个交点,点E(t,n)是抛物线上的动点,四边形OEDC的面积为S.当S取何值时,满足条件的点E只有一个?当S取何值时,满足条件的点E有两个?
查看答案和解析>>
科目:czsx
来源:
题型:
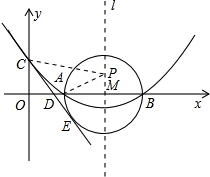
(2013•遵义)如图,已知抛物线y=ax
2+bx+c(a≠0)的顶点坐标为(4,-
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的解析式及A,B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知抛物线y=-x
2+bx+c与x轴的两个交点分别为A(x
1,0),B(x
2,0),且x
1+x
2=4

,
=.
(1)分别求出A,B两点的坐标;
(2)求此抛物线的函数解析式;
(3)设此抛物线与y轴的交点为C,过
=作直线l与抛物线交于另一点D(点D在x轴上方),连接AC,CB,BD,DA,当四边形ACBD的面积为4时,求点D的坐标和直线l的函数解析式.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知抛物线y=ax
2+bx+3与x轴、y轴分别交于A(1,0)、B(0,3)两点,x轴上有一点C
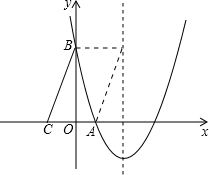
(-1,0),把△BOC向右平移2个单位长度后,一条直角边恰好在抛物线的对称轴上.
(1)求二次函数的关系式;
(2)把△BOC继续向右平移,当B在抛物线上时,求第二次平移的距离.
查看答案和解析>>


![]() 分别交x轴、y轴于点E、F,问△BDC与△EOF是否有可能全等,如果可能,请证明;如果不可能,请说明理由.
分别交x轴、y轴于点E、F,问△BDC与△EOF是否有可能全等,如果可能,请证明;如果不可能,请说明理由.
 如图,已知抛物线与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3).
如图,已知抛物线与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3).
 如图,已知抛物线y=-
如图,已知抛物线y=- (2008•海口一模)如图,已知抛物线经过原点O和点A,点B(2,3)是该抛物线对称轴上一点,过点B作BC∥x轴交抛物线于点C,连接BO、CA,若四边形OACB是平行四边形.
(2008•海口一模)如图,已知抛物线经过原点O和点A,点B(2,3)是该抛物线对称轴上一点,过点B作BC∥x轴交抛物线于点C,连接BO、CA,若四边形OACB是平行四边形. (2013•桐乡市一模)如图,已知抛物线y=ax2+bx+c(a>0)的顶点坐标为(2,-3),将此抛物线在x轴下方的部分沿x轴往上翻折,得到一个新的函数图象(即图中的实线型图象).若|ax2+bx+c|=k(k≠0)时,对应的x的值是两个不相等的实数,则常数k的取值范围是
(2013•桐乡市一模)如图,已知抛物线y=ax2+bx+c(a>0)的顶点坐标为(2,-3),将此抛物线在x轴下方的部分沿x轴往上翻折,得到一个新的函数图象(即图中的实线型图象).若|ax2+bx+c|=k(k≠0)时,对应的x的值是两个不相等的实数,则常数k的取值范围是 如图,已知抛物线过点A(0,6),B(2,0),C(7,
如图,已知抛物线过点A(0,6),B(2,0),C(7, 如图,已知抛物线y=-x2+mx+3与x轴的一个交点A(3,0).
如图,已知抛物线y=-x2+mx+3与x轴的一个交点A(3,0). (2011•梅州)如图,已知抛物线y=x2-4x+3与x 轴交于两点A、B,其顶点为C.
(2011•梅州)如图,已知抛物线y=x2-4x+3与x 轴交于两点A、B,其顶点为C. 如图,已知抛物线y=
如图,已知抛物线y= 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8). (2,0).
(2,0). 如图,已知抛物线y=ax2+c交x轴于点A(-1,0)和点B,交y轴于点C(0,-1).
如图,已知抛物线y=ax2+c交x轴于点A(-1,0)和点B,交y轴于点C(0,-1). 如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),
如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2), 如图,已知抛物线过点A(0,6),B(2,0),C(6,0),直线AB交抛物线的对称轴于点F,直线AC交抛物线对称轴于点E.
如图,已知抛物线过点A(0,6),B(2,0),C(6,0),直线AB交抛物线的对称轴于点F,直线AC交抛物线对称轴于点E. (2013•和平区二模)如图,已知抛物线y=ax2+bx-2经过点A(2,3),B(6,1).
(2013•和平区二模)如图,已知抛物线y=ax2+bx-2经过点A(2,3),B(6,1). (2013•遵义)如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,-
(2013•遵义)如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,- ,
, (-1,0),把△BOC向右平移2个单位长度后,一条直角边恰好在抛物线的对称轴上.
(-1,0),把△BOC向右平移2个单位长度后,一条直角边恰好在抛物线的对称轴上.