
科目:czsx 来源:2011—2012学年江苏无锡育才中学第二学期第一次模拟考试数学卷(带解析) 题型:解答题
已知:矩形纸片ABCD中,AB=26厘米,BC=18.5厘米,点E在AD上,且AE=6厘米,点P是AB边上一动点.按如下操作:
步骤一,折叠纸片,使点P与点E重合,展开纸片得折痕MN(如图1所示);
步骤二,过点P作PT⊥AB,交MN所在的直线于点Q,连接QE(如图2所示)
【小题1】无论点P在AB边上任何位置,都有PQ_________QE(填“ ”、“
”、“ ”、“
”、“ ”号);
”号);
【小题2】如图3所示,将纸片ABCD放在直角坐标系中,按上述步骤一、二进行操作:
①当点P在A点时,PT与MN交于点Q1,Q1点的坐标是(_______,_________);
②当PA=6厘米时,PT与MN交于点Q2. Q2点的坐标是(_______,_________);
③当PA=12厘米时,在图3中画出MN,PT(不要求写画法),并求出MN与PT的交点Q3的坐标;
【小题3】点P在运动过程,PT与MN形成一系列的交点Q1,Q2,Q3……观察、猜想:众多的交点形成的图象是什么?并直接写出该图象的函数表达式.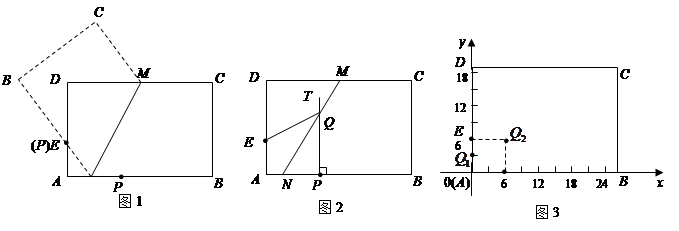
科目:czsx 来源: 题型:
 ”、“
”、“ ”、“
”、“ ”号);
”号);
科目:czsx 来源: 题型:
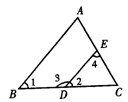
如图4所示,因为∠1=∠2(已知),所以______∥______(______________________).
∠3和∠4是直线______和______被直线_______所截的________角;∠1和∠3是直线_____和______被直线______所截的_______角.
因为∠1=45°,∠3=135°(已知),
所以AB∥DE.(_______________________________)
科目:czsx 来源:同步题 题型:解答题
 表示。在正常水位时水面AB的宽为20m,如果水位上升3m时,水面CD的宽是10m。
表示。在正常水位时水面AB的宽为20m,如果水位上升3m时,水面CD的宽是10m。
科目:czsx 来源: 题型:
 ),B(-2,0).
),B(-2,0).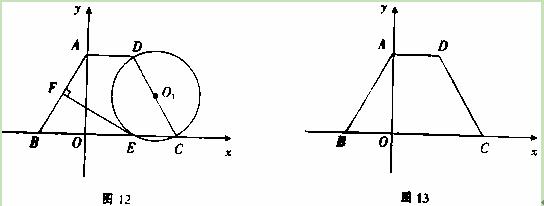
科目:czsx 来源:2011年初中毕业升学考试(湖南娄底卷)数学 题型:解答题
(本小题10分)在等腰梯形ABCD中,AD∥BC,且AD=2,以CD为直径作⊙
O1,交BC于点E,过点E作EF⊥AB于F,建立如图12所示的平面直角坐标系,已知A,
B两点的坐标分别为A(0,2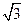 ),B(-2,0).
),B(-2,0).
(1)求C,D两点的坐标.
(2)求证:EF为⊙O1的切线.
(3)探究:如图13,线段CD上是否存在点P,使得线段PC的长度与P点到y轴的距离相等?如果存在,请找出P点的坐标;如果不存在,请说明理由.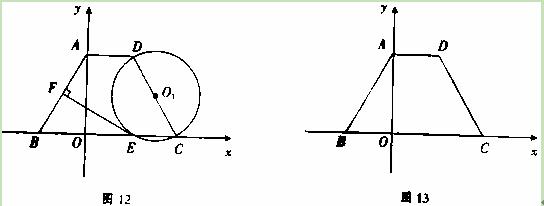
科目:czsx 来源:2011年初中毕业升学考试(四川内江卷)数学 题型:解答题
(本小题10分)在等腰梯形ABCD中,AD∥BC,且AD=2,以CD为直径作⊙
O1,交BC于点E,过点E作EF⊥AB于F,建立如图12所示的平面直角坐标系,已知A,
B两点的坐标分别为A(0,2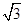 ),B(-2,0).
),B(-2,0).
(1)求C,D两点的坐标.
(2)求证:EF为⊙O1的切线.
(3)探究:如图13,线段CD上是否存在点P,使得线段PC的长度与P点到y轴的距离相等?如果存在,请找出P点的坐标;如果不存在,请说明理由.
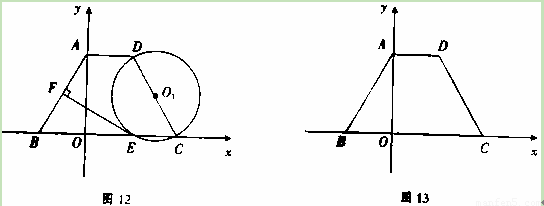
科目:czsx 来源: 题型:
(本小题10分)在等腰梯形ABCD中,AD∥BC,且AD=2,以CD为直径作⊙
O1,交BC于点E,过点E作EF⊥AB于F,建立如图12所示的平面直角坐标系,已知A,
B两点的坐标分别为A(0,2![]() ),B(-2,0).
),B(-2,0).
(1)求C,D两点的坐标.
(2)求证:EF为⊙O1的切线.
(3)探究:如图13,线段CD上是否存在点P,使得线段PC的长度与P点到y轴的距离相等?如果存在,请找出P点的坐标;如果不存在,请说明理由.
科目:czsx 来源: 题型:
如图5所示,
①因为∠1=∠C(已知),所以ED∥______.(__________)
②因为∠2=∠BED(已知),所以DF∥_______.(_________)
③因为∠3=∠B(已知),所以_____∥______(__________)
④因为∠2+∠AFD=180°(已知),所以_____∥______.(__________)
⑤因为∠DFC=∠C_____(已知),所以ED∥AC.(_________)

科目:czsx 来源: 题型:
如图1所示,因为∠1=∠2(已知),所以_____∥_____.(__________________)
因为∠2=∠3(已知),所以_____∥______.(__________________________)

科目:czsx 来源: 题型:022
看图填空.
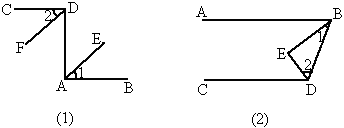
(1)如图(1)所示,因为AB⊥AD,CD⊥AD(已知),所以______=_______=90°( ).
又因为∠1=∠2(已知),所以∠BAD-∠1=∠CDA-∠2,即∠ADF=∠DAE.所以_______∥________( ).
(2)如图(2)所示,因为BE平分∠ABD(已知),所以______=2∠1( ).因为DE平分∠BDC(已知),所以________=2∠2( ).所以______+_______=2∠1+2∠2=2(∠1+∠2).
又因为∠1+∠2=90°(已知),所以_______+_______=2×90°=180°,所以_______∥_______( ).
科目:czsx 来源:活学巧练 九年级数学 下 题型:044
如图,有一座抛物线型拱桥,桥下面正常水位时AB宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m.

(1)在如图的坐标系中求抛物线的表达式.
(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶?
科目:czsx 来源: 题型:044
如图,有一座抛物线型拱桥,桥下面正常水位时AB宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m.
(1)
在如图的坐标系中求抛物线的表达式.(2)
若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶?

科目:czsx 来源:北京同步题 题型:解答题

科目:czsx 来源: 题型:
 0m.建立如图所示的直角坐标系,则此抛物线的解析式为
0m.建立如图所示的直角坐标系,则此抛物线的解析式为科目:czsx 来源: 题型:
 上升3米,则水面CD的宽是10米.
上升3米,则水面CD的宽是10米.科目:czsx 来源: 题型:
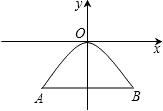 如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为10m,此时水面到桥拱的距离是4m,则抛物线的函数关系式为( )
如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为10m,此时水面到桥拱的距离是4m,则抛物线的函数关系式为( )A、y=
| ||
B、y=-
| ||
C、y=-
| ||
D、y=
|
科目:czsx 来源: 题型:
科目:czsx 来源:《第26章 二次函数》2010年复习题(解析版) 题型:解答题
科目:czsx 来源:2010-2011学年北京市平谷区初三第一学期期末数学卷 题型:解答题
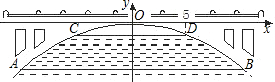
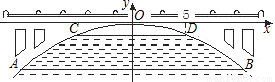
如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20米,如果水位上升3米,则水面CD的宽是10米.

(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)当水位在正常水位时,有一艘宽为6米的货船经过这里,船舱上有高出水面3.6米的长方体货物(货物与货船同宽).问:此船能否顺利通过这座拱桥?