科目：czsx
来源：同步题
题型：证明题
如图：已知AE交BC于点D，∠1=∠2=∠3，AB=AD。求证：DC=BE。
查看答案和解析>>
科目：czsx
来源：
题型：阅读理解
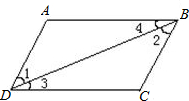
23、阅读填空：
（1）如图，请你完成小颖和小明的说理过程：
小颖：
因为AD与BC是平行的，所以∠1=
∠2
，理由是
两直线平行，内错角相等
．
小明：
∠3=∠4→
AB
∥
CD
→∠A+
ADC
=180°
其中第一步的理由是
内错角相等，两直线平行
第二步的理由是
两直线平行，同旁内角互补
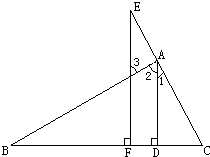
（2）如图：已知：AD⊥BC于D，EF⊥BC于F，∠1=∠3，
求证：AD平分∠BAC．
证明：∵AD⊥BC 于D
EF⊥BC于F（已知）
∴AD∥EF
同垂直于一条直线的两直线平行
∴∠1=∠E
两直线平行，同位角相等
∠2=∠3
两直线平行，内错角相等
又∵∠3=∠1（已知）
∴∠1=∠2
等量代换
∴AD平分∠BAC
角平分线定义
．
查看答案和解析>>
科目：czsx
来源：
题型：
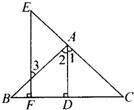
21、补全下列证明过程及括号内的推理依据：
如图，已知：AD⊥BC于D，EF⊥BC于F，∠3=∠E，求证：AD平分∠BAC．
证明：∵AD⊥BC，EF⊥BC（已知）．
∴AD∥
EF
（在同一平面内，垂直于同一条直线的两条直线互相平行），
∴∠1=∠E（
两直线平行，同位角相等
），
∠2=∠3（
两直线平行，内错角相等
）
又∵∠3=∠E（已知），
∴∠1=∠2（等量代换），
∴AD平分∠BAC（
角平分线的定义
）
查看答案和解析>>
科目：czsx
来源：2013届河北省承德地区八年级上学期期中考试数学卷
题型：选择题
如图，已知： AC⊥BC于C , DE⊥AC于E , AD⊥AB于A , BC=AE．若AB=5 ,AD= 。
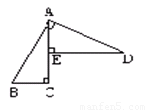
查看答案和解析>>
科目：czsx
来源：
题型：
如图，已知： AC⊥BC于C , DE⊥AC于E , AD⊥AB于A , BC=AE．若AB="5" ,AD=
。
查看答案和解析>>
科目：czsx
来源：
题型：填空题
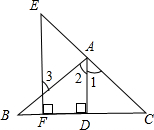补全下列证明过程及括号内的推理依据：
如图，已知：AD⊥BC于D，EF⊥BC于F，∠3=∠E，求证：AD平分∠BAC．
证明：∵AD⊥BC，EF⊥BC（已知）．
∴AD∥________（在同一平面内，垂直于同一条直线的两条直线互相平行），
∴∠1=∠E（________），
∠2=∠3（________）
又∵∠3=∠E（已知），
∴∠1=∠2（等量代换），
∴AD平分∠BAC（________）
查看答案和解析>>
科目：czsx
来源：河北省承德地区2011-2012学年八年级上学期期中考试数学试题
题型：022
如图，已知：AC⊥BC于C，DE⊥AC于E，AD⊥AB于A，BC＝AE．若AB＝5，AD＝_______．
查看答案和解析>>
科目：czsx
来源：101网校同步练习 初一数学 北师大(新课标2001/3年初审) 北师大(新课标2001/3年初审)
题型：022
如图，已知，AD⊥BC于D，DE⊥AB于E，点F是AE的中点，则图中有( )个三角形，( )个直角三角形，( )个锐角三角形，( )个钝角三角形，以∠B为内角的三角形有( )个，以BE为一边的三角形是( )．
查看答案和解析>>
科目：czsx
来源：2011-2012学年河北省承德地区八年级上学期期中考试数学卷
题型：填空题
如图，已知： AC⊥BC于C , DE⊥AC于E , AD⊥AB于A , BC=AE．若AB="5" ,AD= 。
查看答案和解析>>
科目：czsx
来源：
题型：
如图，已知： AC⊥BC于C , DE⊥AC于E , AD⊥AB于A , BC=AE．若AB=5 ,AD= 。
查看答案和解析>>
科目：czsx
来源：
题型：
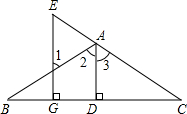
如图，已知：AD⊥BC于D，EG⊥BC于G，∠E=∠1．求证：AD平分∠BAC．
下面是部分推理过程，请你将其补充完整：
∵AD⊥BC于D，EG⊥BC于G （已知）
∴∠ADC=∠EGC=90°
∴AD∥EG
同位角相等，两直线平行
同位角相等，两直线平行
．
∴∠1=∠2
两直线平行，内错角相等
两直线平行，内错角相等
．
∠E
∠E
=∠3（两直线平行，同位角相等）
又∵∠E=∠1（已知）
∴∠2=∠3
等量代换
等量代换
．
∴AD平分∠BAC
角平分线的定义
角平分线的定义
．
查看答案和解析>>
科目：czsx
来源：
题型：
如图，已知：AD⊥BC于D，EG⊥BC于G，∠E=∠1．求证：AD平分∠BAC．
查看答案和解析>>
科目：czsx
来源：
题型：
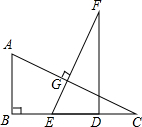
如图，已知：AB⊥BC于B，EF⊥AC于G，DF⊥BC于D，BC=DF．求证：AC=EF．
查看答案和解析>>
科目：czsx
来源：
题型：解答题
（1）如图，请你完成小颖和小明的说理过程：
小颖：
因为AD与BC是平行的，所以∠1=______，理由是______．
小明：
∠3=∠4→______∥______→∠A+______=180°
其中第一步的理由是______
第二步的理由是______
（2）如图：已知：AD⊥BC于D，EF⊥BC于F，∠1=∠3，
求证：AD平分∠BAC．
证明：∵AD⊥BC 于D
EF⊥BC于F（已知）
∴AD∥EF______
∴∠1=∠E______
∠2=∠3______
又∵∠3=∠1（已知）
∴∠1=∠2______
∴AD平分∠BAC______．
查看答案和解析>>
科目：czsx
来源：
题型：
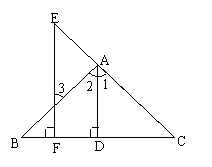
填空(补全下列证明及括号内的推理依据)：
如图：已知：AD⊥BC于D，EF⊥BC于F，∠1=∠3，
求证：AD平分∠BAC。
证明：∵AD⊥BC，EF⊥BC于F(已知)
∴AD∥EF( )
∴∠1=∠E( )
∠2=∠3( )
又∵∠3=∠1(已知)
∴∠1=∠2(等量代换)
∴AD平分∠BAC( )
查看答案和解析>>
科目：czsx
来源：
题型：
如图，已知：AD⊥BC于D，EG⊥BC于G，∠E=∠1．求证：AD平分∠BAC．
下面是部分推理过程，请你将其补充完整：
∵AD⊥BC于D，EG⊥BC于G （已知）
∴∠ADC=∠EGC=90°
∴AD∥EG（ ）
∴∠1=∠2（ ）
=∠3（两直线平行，同位角相等）
又∵∠E=∠1（已知）
∴∠2=∠3（ ）
∴AD平分∠BAC（ ）
查看答案和解析>>
科目：czsx
来源：
题型：
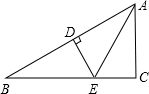
如图，已知DE垂直平分AB，分别交AB、BC于D、E两点，AE平分∠BAC，∠B=30°，BE=4，求AC的长．
查看答案和解析>>
科目：czsx
来源：2005年全国中考数学试题汇编《三角形》（10）（解析版）
题型：解答题
（2005•岳阳）如图，已知DE垂直平分AB，分别交AB、BC于D、E两点，AE平分∠BAC，∠B=30°，BE=4，求AC的长．
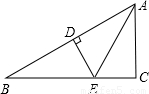
查看答案和解析>>
科目：czsx
来源：
题型：解答题
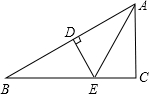如图，已知DE垂直平分AB，分别交AB、BC于D、E两点，AE平分∠BAC，∠B=30°，BE=4，求AC的长．
查看答案和解析>>
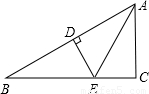
科目：czsx
来源：2005年湖南省岳阳市中考数学试卷（课标卷）（解析版）
题型：解答题
（2005•岳阳）如图，已知DE垂直平分AB，分别交AB、BC于D、E两点，AE平分∠BAC，∠B=30°，BE=4，求AC的长．
查看答案和解析>>
