科目:czsx
来源:
题型:
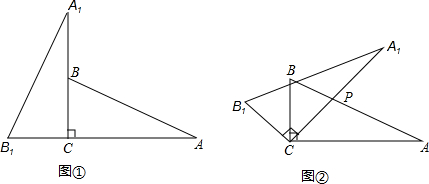
将两块含 30°角且大小相同的直角三角板如图①摆放,将图①中△A
1B
1C 绕点 C 顺时针旋转 45°得图②,点 P 是 A
1C 与 AB 的交点,若 AP=2,求 C P 的长.
查看答案和解析>>
科目:czsx
来源:
题型:
将两块含30°角且大小相同的直角三角板如图1摆放.
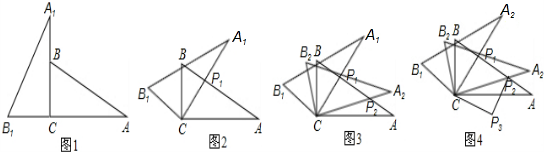
(1)将图1中△A
1B
1C绕点C顺时针旋转45°得图2,点P
1是A
1C与AB的交点,求证:CP
1=
AP
1;
(2)将图2中△A
1B
1C绕点C顺时针旋转30°到△A
2B
2C(如图3),点P
2是A
2C与AB的交点.线段CP
1与P
1P
2之间存在一个确定的等量关系,请你写出这个关系式并说明理由;
(3)将图3中线段CP
1绕点C顺时针旋转60°到CP
3(如图4),连接P
3P
2,求证:P
3P
2⊥AB.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
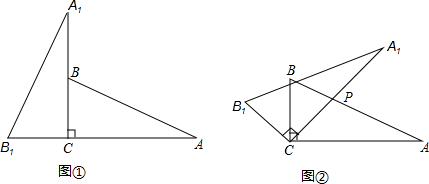
将两块含 30°角且大小相同的直角三角板如图①摆放,将图①中△A1B1C 绕点 C 顺时针旋转 45°得图②,点 P 是 A1C 与 AB 的交点,若 AP=2,求 C P 的长.
查看答案和解析>>
科目:czsx
来源:初中数学 三点一测丛书 八年级数学 下 (江苏版课标本) 江苏版
题型:047
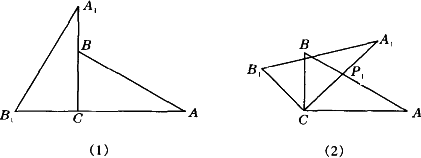
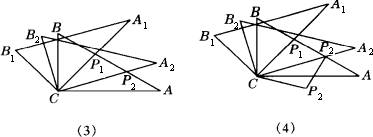
将两块含30°角且大小相同的直角三角板如图摆放.
(1)将图(1)中△A1B1C绕点C顺时针旋转45°得图(2),点P1是A1C与AB的交点,求证:CP1=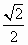 AP1;
AP1;
(2)将图(2)中△A1B1C绕点C顺时针旋转30°到△A2B2C(如图(3)),P2是A2C与AB的交点,线段CP1与P1P2之间存在一个确定的等量关系,请你写出这个关系式并说明理由;
(3)将图(3)中线段CP1绕点C顺时针旋转60°到CP3(如图(4)),连结P3P2,求证:P3P2⊥AB.
查看答案和解析>>
科目:czsx
来源:
题型:
将两块含30°角且大小相同的直角三角板如图l摆放。

(1)将图l中△A1B1C绕点C顺时针转45°得到图2,点Pl是A1C与AB的交点,求证: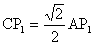
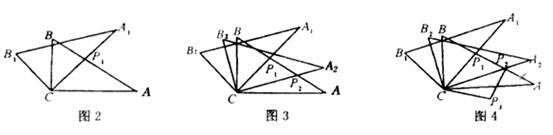
(2)将图2中△A1B1C绕点C顺时针旋转30°到△A2B2C(如图3),P2是A2C与AB的交点,线段CP1与P1P2之间存在一个确定的等量关系,请你写出这个等量关系式,并说明理由;
(3)将图3中线段CP1绕点C顺时针旋转60°到CP3(如图4)连结P3P2,求证:P3P2⊥AB。
查看答案和解析>>
科目:czsx
来源:2006年初中数学总复习下册
题型:044
将两块含30°角且大小相同的直角三角板如图1摆放.
(1)将图1中△A1B1C绕点C顺时针旋转45°得图2,点P是A1C与AB的交点,求证:CP1=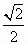 AP1;
AP1;
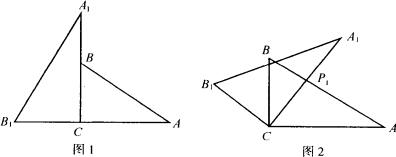
(2)将图2中△A1B1C绕点C顺时针旋转30°到△A2B2C(如图3),P2是A2C与AB的交点,线段CP1与P1P2之间存在一个确定的等量关系,请你写出这个关系式并说明理由;
(3)将图3中线段CP1绕点C顺时针旋转60°到CP3(如图4),连结P3P2,求证:P3P2⊥AB.
查看答案和解析>>
科目:czsx
来源:专项题
题型:解答题
将两块含30°角且大小相同的直角三角板如图①摆放,将图①中△A1B1C(绕点C顺时针旋转45°得到图②,点P是A1C与AB的交点,若AP=2,求CP的长。
查看答案和解析>>
科目:czsx
来源:2011-2012学年广东省珠海市文园中学九年级(上)期中数学试卷(解析版)
题型:解答题
将两块含30°角且大小相同的直角三角板如图1摆放.

(1)将图1中△A
1B
1C绕点C顺时针旋转45°得图2,点P
1是A
1C与AB的交点,求证:CP
1=
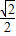
AP
1;
(2)将图2中△A
1B
1C绕点C顺时针旋转30°到△A
2B
2C(如图3),点P
2是A
2C与AB的交点.线段CP
1与P
1P
2之间存在一个确定的等量关系,请你写出这个关系式并说明理由;
(3)将图3中线段CP
1绕点C顺时针旋转60°到CP
3(如图4),连接P
3P
2,求证:P
3P
2⊥AB.
查看答案和解析>>
科目:czsx
来源:2005年全国中考数学试题汇编《三角形》(15)(解析版)
题型:解答题
(2005•武汉)将两块含30°角且大小相同的直角三角板如图1摆放.

(1)将图1中△A
1B
1C绕点C顺时针旋转45°得图2,点P
1是A
1C与AB的交点,求证:CP
1=
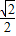
AP
1;
(2)将图2中△A
1B
1C绕点C顺时针旋转30°到△A
2B
2C(如图3),点P
2是A
2C与AB的交点.线段CP
1与P
1P
2之间存在一个确定的等量关系,请你写出这个关系式并说明理由;
(3)将图3中线段CP
1绕点C顺时针旋转60°到CP
3(如图4),连接P
3P
2,求证:P
3P
2⊥AB.
查看答案和解析>>
科目:czsx
来源:第26章《圆》中考题集(08):26.1 旋转(解析版)
题型:解答题
将两块含30°角且大小相同的直角三角板如图1摆放.
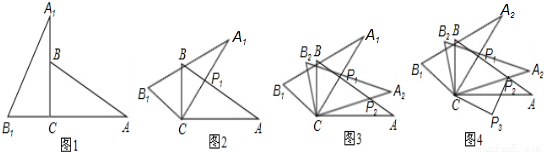
(1)将图1中△A
1B
1C绕点C顺时针旋转45°得图2,点P
1是A
1C与AB的交点,求证:CP
1=

AP
1;
(2)将图2中△A
1B
1C绕点C顺时针旋转30°到△A
2B
2C(如图3),点P
2是A
2C与AB的交点.线段CP
1与P
1P
2之间存在一个确定的等量关系,请你写出这个关系式并说明理由;
(3)将图3中线段CP
1绕点C顺时针旋转60°到CP
3(如图4),连接P
3P
2,求证:P
3P
2⊥AB.
查看答案和解析>>
科目:czsx
来源:2005年湖北省武汉市中考数学试卷(课标卷)(解析版)
题型:解答题
(2005•武汉)将两块含30°角且大小相同的直角三角板如图1摆放.
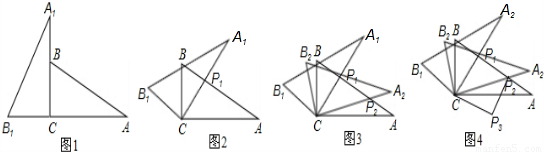
(1)将图1中△A
1B
1C绕点C顺时针旋转45°得图2,点P
1是A
1C与AB的交点,求证:CP
1=

AP
1;
(2)将图2中△A
1B
1C绕点C顺时针旋转30°到△A
2B
2C(如图3),点P
2是A
2C与AB的交点.线段CP
1与P
1P
2之间存在一个确定的等量关系,请你写出这个关系式并说明理由;
(3)将图3中线段CP
1绕点C顺时针旋转60°到CP
3(如图4),连接P
3P
2,求证:P
3P
2⊥AB.
查看答案和解析>>
科目:czsx
来源:第25章《图形的变换》中考题集(17):25.2 旋转变换(解析版)
题型:解答题
将两块含30°角且大小相同的直角三角板如图1摆放.
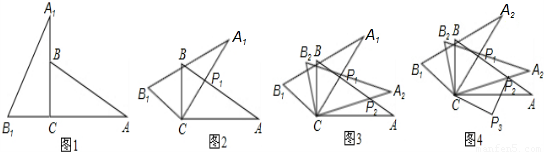
(1)将图1中△A
1B
1C绕点C顺时针旋转45°得图2,点P
1是A
1C与AB的交点,求证:CP
1=
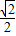
AP
1;
(2)将图2中△A
1B
1C绕点C顺时针旋转30°到△A
2B
2C(如图3),点P
2是A
2C与AB的交点.线段CP
1与P
1P
2之间存在一个确定的等量关系,请你写出这个关系式并说明理由;
(3)将图3中线段CP
1绕点C顺时针旋转60°到CP
3(如图4),连接P
3P
2,求证:P
3P
2⊥AB.
查看答案和解析>>
科目:czsx
来源:第23章《旋转》中考题集(06):23.1 图形的旋转(解析版)
题型:解答题
将两块含30°角且大小相同的直角三角板如图1摆放.

(1)将图1中△A
1B
1C绕点C顺时针旋转45°得图2,点P
1是A
1C与AB的交点,求证:CP
1=

AP
1;
(2)将图2中△A
1B
1C绕点C顺时针旋转30°到△A
2B
2C(如图3),点P
2是A
2C与AB的交点.线段CP
1与P
1P
2之间存在一个确定的等量关系,请你写出这个关系式并说明理由;
(3)将图3中线段CP
1绕点C顺时针旋转60°到CP
3(如图4),连接P
3P
2,求证:P
3P
2⊥AB.
查看答案和解析>>
科目:czsx
来源:2008-2009学年福建省三明市清流县九年级(上)期中数学试卷(解析版)
题型:解答题
将两块含 30°角且大小相同的直角三角板如图①摆放,将图①中△A
1B
1C 绕点 C 顺时针旋转 45°得图②,点 P 是 A
1C 与 AB 的交点,若 AP=2,求 C P 的长.

查看答案和解析>>
科目:czsx
来源:2005年全国中考数学试题汇编《图形的旋转》(03)(解析版)
题型:解答题
(2005•武汉)将两块含30°角且大小相同的直角三角板如图1摆放.

(1)将图1中△A
1B
1C绕点C顺时针旋转45°得图2,点P
1是A
1C与AB的交点,求证:CP
1=
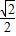
AP
1;
(2)将图2中△A
1B
1C绕点C顺时针旋转30°到△A
2B
2C(如图3),点P
2是A
2C与AB的交点.线段CP
1与P
1P
2之间存在一个确定的等量关系,请你写出这个关系式并说明理由;
(3)将图3中线段CP
1绕点C顺时针旋转60°到CP
3(如图4),连接P
3P
2,求证:P
3P
2⊥AB.
查看答案和解析>>
科目:czsx
来源:2012届江苏省泰州市永安初级中学九年级3月练习数学试题(带解析)
题型:填空题
将两块含30°角的直角三角尺的直角顶点重合,放置为如图的形状,若∠AOD=110°,则∠COB = °. 
查看答案和解析>>
科目:czsx
来源:2011-2012学年江苏省泰州市九年级3月练习数学试题(解析版)
题型:填空题
将两块含30°角的直角三角尺的直角顶点重合,放置为如图的形状,若∠AOD=110°,则∠COB =
°.

查看答案和解析>>
科目:czsx
来源:江苏模拟题
题型:填空题
将两块含30°角的直角三角尺的直角顶点重合,放置为如图的形状,若∠AOD=110°,则∠COB=( )°。
查看答案和解析>>
科目:czsx
来源:
题型:
将两块含30°角的直角三角尺的直角顶点重合,放置为如图的形状,若∠AOD=110°,则∠COB = °.
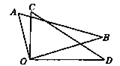
查看答案和解析>>
科目:czsx
来源:
题型:
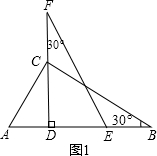
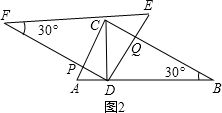
如图1,我们将相同的两块含30°角的直角三角板Rt△DEF与Rt△ABC叠合,使DE在AB上,DE过点C,已知AC=DE=6.
(1)将图1中的△DEF绕点D逆时针旋转(DF与AB不重合),使边DF、DE分别交AC、BC于点P、Q,如图2.
①求证:△CQD∽△APD;
②连接PQ,设AP=x,求面积S
△PCQ关于x的函数关系式;
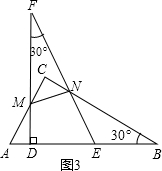
(2)将图1中的△DEF向左平移(点A、D不重合),使边FD、FE分别交AC、BC于点M、N设AM=t,如图3.
①判断△BEN是什么三角形?并用含t的代数式表示边BE和BN;
②连接MN,求面积S
△MCN关于t的函数关系式;
(3)在旋转△DEF的过程中,试探求AC上是否存在点P,使得S
△PCQ等于平移所得S
△MCN的最大值?说明你的理由.
查看答案和解析>>




![]() AP1;
AP1;


![]()

![]() AP1;
AP1;



 AP1;
AP1;
 AP1;
AP1;
 AP1;
AP1;
 AP1;
AP1;
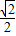 AP1;
AP1;
 AP1;
AP1;

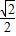 AP1;
AP1;



