=关于x的方程2x2+3x-m+1=0的两个实数根的倒数和为3，求m的值答案解析
科目：czsx
来源：
题型：
关于x的方程2x
2-2x+3m-1=0有两个实数根x
1，x
2，且x
1x
2＞x
1+x
2-4，则实数m的取值范围是
．
查看答案和解析>>
科目：czsx
来源：不详
题型：填空题
关于x的方程2x2-2x+3m-1=0有两个实数根x1，x2，且x1x2＞x1+x2-4，则实数m的取值范围是______．
查看答案和解析>>
科目：czsx
来源：
题型：填空题
关于x的方程2x2-2x+3m-1=0有两个实数根x1，x2，且x1x2＞x1+x2-4，则实数m的取值范围是________．
查看答案和解析>>
科目：czsx
来源：中华题王 数学 九年级上 (北师大版) 北师大版
题型：044
解下题：
关于x的方程2x2－7x＋m＝0的两个实数根互为倒数，求m的值．
查看答案和解析>>
科目：czsx
来源：期中题
题型：单选题
如果关于x的方程2x2-7x=m=0的两个实数根互为倒数，那么m的值为
查看答案和解析>>
科目：czsx
来源：
题型：
关于x的方程x
2-x-k=0有两个实数根，则k的取值范围是
．
查看答案和解析>>
科目：czsx
来源：
题型：
已知以x为自变量的二次函数y=x2+2mx+m-7．
（1）求证：不论m为任何实数，二次函数的图象与x轴都有两个交点；
（2）若二次函数的图象与x轴的两个交点在点（1，0）的两侧，关于x的一元二次方程m2x2+（2m+3）x+1=0有两个实数根，且m为整数，求m的值；
（3）在（2）的条件下，关于x的另一方程x2+2（a+m）x+2a-m2+6 m-4=0有大于0且小于5的实数根，求a的整数值．
查看答案和解析>>
科目：czsx
来源：
题型：
若关于x的方程（a2-3）x2-2（a-2）x+1=0的两个实数根互为倒数，求a的值．
查看答案和解析>>
科目：czsx
来源：
题型：
（2011•崇川区模拟）关于x的一元二次方程x
2-4x+k+2=0有两个实数根，且k为正整数．
（1）求k的值；
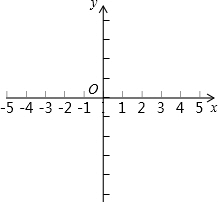
（2）当此方程有两个不相等的实数根时，将关于x的二次函数y=x
2-4x+k+2的图象向下平移3个单位，求平移后图象的解析式，并在所给的直角坐标系中描点画出它的图象．
查看答案和解析>>
科目：czsx
来源：
题型：
已知关于x的方程
kx2-x+1=0有两个实数根．
（1）求k的取值范围．
（2）抛物线y=
kx2-x+1与x轴的交能否都在y轴的左边？请作出决断并说明理由．
查看答案和解析>>
科目：czsx
来源：
题型：
已知关于x的方程k2x2+（2k-1）x+1=0两个实数根互为倒数，那么k的值为（ ）
查看答案和解析>>
科目：czsx
来源：
题型：
23、已知：关于x的方程x2-6x+8-t=0有两个实数根，且y=（x1-2）（x2-2），请求出y与t的函数关系式．
查看答案和解析>>
科目：czsx
来源：
题型：
如果关于x的一元二次方程2x
2-2x+3m-1=0有两个实数根x
1，x
2，且它们满足不等式
＜1，则实数m的取值范围是
．
查看答案和解析>>
科目：czsx
来源：
题型：
已知方程x2-3x+a+4=0有两个整数根．
（1）求证：这两个整数根一个是奇数根，一个是偶数根；
（2）求证：a是负数；
（3）当方程的两个整数根同号时，求a的值及这两个根．
查看答案和解析>>
科目：czsx
来源：
题型：
已知关于x的一元二次方程
x2-x+m=0有两个实数根，若m为正整数，求此方程的根．
查看答案和解析>>
科目：czsx
来源：
题型：
已知一元二次方程x
2-3x-2=0的两个实数根是a和b，不解方程，求：（1）
+
；（2）a
2+b
2．
查看答案和解析>>
科目：czsx
来源：
题型：
已知关于x的方程（a
2-1）x
2-（a+1）x+1=0的两个实数根互为倒数，则a的值为
．
查看答案和解析>>
科目：czsx
来源：
题型：解答题
关于x的一元二次方程x2-4x+k+2=0有两个实数根，且k为正整数．
（1）求k的值；
（2）当此方程有两个不相等的实数根时，将关于x的二次函数y=x2-4x+k+2的图象向下平移3个单位，求平移后图象的解析式，并在所给的直角坐标系中描点画出它的图象．
查看答案和解析>>
科目：czsx
来源：2013-2014学年江苏大丰刘庄第二初级中学九年级上学期期末模拟数学试卷（解析版）
题型：选择题
关于x的方程kx2+2x－1=0有两个实数根，则k的取值范围是
A．k≥1 B．k≥－1
C．k≥1且k≠0 D．k≥－1且k≠0
查看答案和解析>>
科目：czsx
来源：2012年沪科版初中数学八年级下19.2一元二次方程的解法练习卷（解析版）
题型：选择题
下列说法错误的是
A.关于x的方程x2=k，必有两个互为相反数的实数根
B.关于x的方程ax2+bx=0(a≠0)必有一根为0
C．关于x的方程(x-c)2=k2必有两个实数根
D．关于x的方程x2=1-a2可能没有实数根
查看答案和解析>>
