科目:czsx
来源:
题型:
已知如图10所示,把一张矩形纸片ABCD沿BD对折,使C点落在E处,BE与AD相交于点O,写出一组相等的线段___________(不包括AB=CD和AD=BC).

查看答案和解析>>
科目:czsx
来源:
题型:
如图1所示,一张半圆形纸片,直径AB=10,点C是半圆上的一个动点.沿半径CO把这张纸片剪出△AC
1O
1和△BC
2O
2两个三角形(如图2所示).将纸片△AC
1O
1沿直线O
2B(AB)方向平移(点A,O
1,O
2,B始终在同一直线上),当点O
1与点B重合时,停止平移.在平移过程中,C
1O
1与BC
2交于点E,AC
1与C
2O
2,BC
2分别交于点F、P.
(1)当△AC
1O
1平移到如图3所示的位置时,猜想图中的O
1E与O
2F的数量关系,并证明你的猜想;
(2)若∠CAB=30°,设平移距离O
1O
2为x,△AC
1O
1与△BC
2O
2重叠部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的x的值,使重叠部分的面积等于原△ABC面积的
.若存在,求x的值;若不存在,请说明理由.
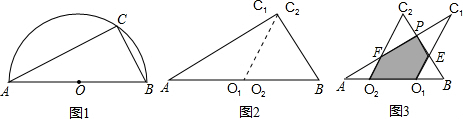
查看答案和解析>>
科目:czsx
来源:
题型:
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成△AC
1D
1和△BC
2D
2两个三角形(如图所示).将纸片△AC
1D
1沿直线D
2B(AB)方向平移(点A,D
1,D
2,B始终在同一直线上),当点D
1于点B重合时,停止平移.在平移过程中,C
1D
1与BC
2交于点E,AC
1与C
2D
2、BC
2分别交于点F、P.
(1)当△AC
1D
1平移到如图3所示的位置时,猜想图中的D
1E与D
2F的数量关系,并证明你的猜想;
(2)设平移距离D
2D
1为x,△AC
1D
1与△BC
2D
2重叠部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的x的值使得y=
S
△ABC;若不存在,请说明理由.
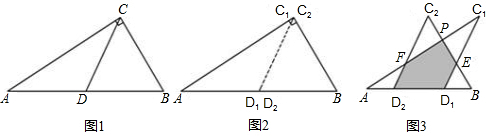
查看答案和解析>>
科目:czsx
来源:
题型:
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8cm,BC=6cm.沿斜边AB的中线CD把这张纸片剪成△AC
1D
1和△BC
2D
2两个三角形(如图2所示).将纸片△AC
1D
1沿直线D
2B(AB)方向平移(点A、D
1、D
2、B始终在同一直线上),当点A与点B重合时,停止平移.设平移的速度是1cm/秒,平移的时间为x(秒),△AC
1D
1与△BC
2D
2重叠部分面积为y(cm
2).

(1)求CD的长和斜边上的高CH;
(2)在平移过程中(如图3),设C
1D
1与BC
2交于点E,AC
1与C
2D
2、BC
2分别交于点F、P.那么四边形FD
2D
1E是否可能是菱形?为什么?如果可能,请求出相应的D
1E=D
2F的值;
(3)请写出y与x的函数关系式,以及自变量的取值范围;
(4)是否存在这样的x的值,使重叠部分面积为3cm
2?若存在,求出相应的x的值;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(41):2.7 最大面积是多少(解析版)
题型:解答题
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成△AC
1D
1和△BC
2D
2两个三角形(如图所示).将纸片△AC
1D
1沿直线D
2B(AB)方向平移(点A,D
1,D
2,B始终在同一直线上),当点D
1于点B重合时,停止平移.在平移过程中,C
1D
1与BC
2交于点E,AC
1与C
2D
2、BC
2分别交于点F、P.
(1)当△AC
1D
1平移到如图3所示的位置时,猜想图中的D
1E与D
2F的数量关系,并证明你的猜想;
(2)设平移距离D
2D
1为x,△AC
1D
1与△BC
2D
2重叠部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的x的值使得y=

S
△ABC;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:2011-2012学年广东汕头龙湖区中考模拟数学试卷(解析版)
题型:解答题
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成△AC1D1和△BC2D2两个三角形(如图2所示).将纸片△AC1D1沿直线D2B(AB)方向平移(点A,D1,D2,B始终在同一直线上),当点D1与点B重合时,停止平移.在平移的过程中,C1D1与BC2交于点E,AC1与C2D2、BC2分别交于点F、P.
1.当△AC1D1平移到如图3所示位置时,猜想D1E与D2F的数量关系,并说明理由
2.设平移距离D2D1为x,△AC1D1和△BC2D2重复部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
3.对于(2)中的结论是否存在这样的x,使得重复部分面积等于原△ABC纸片面积的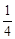 ?若存在,请求出x的值;若不存在,请说明理由.
?若存在,请求出x的值;若不存在,请说明理由.
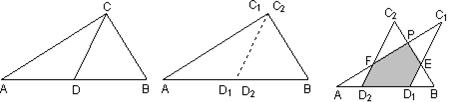
图1
图2
图3
查看答案和解析>>
科目:czsx
来源:第26章《二次函数》中考题集(41):26.3 实际问题与二次函数(解析版)
题型:解答题
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成△AC
1D
1和△BC
2D
2两个三角形(如图所示).将纸片△AC
1D
1沿直线D
2B(AB)方向平移(点A,D
1,D
2,B始终在同一直线上),当点D
1于点B重合时,停止平移.在平移过程中,C
1D
1与BC
2交于点E,AC
1与C
2D
2、BC
2分别交于点F、P.
(1)当△AC
1D
1平移到如图3所示的位置时,猜想图中的D
1E与D
2F的数量关系,并证明你的猜想;
(2)设平移距离D
2D
1为x,△AC
1D
1与△BC
2D
2重叠部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的x的值使得y=

S
△ABC;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:2013年重庆市西南大学附属中学中考数学二模试卷(解析版)
题型:解答题
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8cm,BC=6cm.沿斜边AB的中线CD把这张纸片剪成△AC
1D
1和△BC
2D
2两个三角形(如图2所示).将纸片△AC
1D
1沿直线D
2B(AB)方向平移(点A、D
1、D
2、B始终在同一直线上),当点A与点B重合时,停止平移.设平移的速度是1cm/秒,平移的时间为x(秒),△AC
1D
1与△BC
2D
2重叠部分面积为y(cm
2).

(1)求CD的长和斜边上的高CH;
(2)在平移过程中(如图3),设C
1D
1与BC
2交于点E,AC
1与C
2D
2、BC
2分别交于点F、P.那么四边形FD
2D
1E是否可能是菱形?为什么?如果可能,请求出相应的D
1E=D
2F的值;
(3)请写出y与x的函数关系式,以及自变量的取值范围;
(4)是否存在这样的x的值,使重叠部分面积为3cm
2?若存在,求出相应的x的值;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2010年天津市中考数学模拟试卷(二)(解析版)
题型:解答题
(2006•重庆)如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成△AC
1D
1和△BC
2D
2两个三角形(如图所示).将纸片△AC
1D
1沿直线D
2B(AB)方向平移(点A,D
1,D
2,B始终在同一直线上),当点D
1于点B重合时,停止平移.在平移过程中,C
1D
1与BC
2交于点E,AC
1与C
2D
2、BC
2分别交于点F、P.
(1)当△AC
1D
1平移到如图3所示的位置时,猜想图中的D
1E与D
2F的数量关系,并证明你的猜想;
(2)设平移距离D
2D
1为x,△AC
1D
1与△BC
2D
2重叠部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的x的值使得y=

S
△ABC;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2013年黑龙江省大庆市三十一中中考数学模拟试卷(一)(解析版)
题型:解答题
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成△AC
1D
1和△BC
2D
2两个三角形(如图所示).将纸片△AC
1D
1沿直线D
2B(AB)方向平移(点A,D
1,D
2,B始终在同一直线上),当点D
1于点B重合时,停止平移.在平移过程中,C
1D
1与BC
2交于点E,AC
1与C
2D
2、BC
2分别交于点F、P.
(1)当△AC
1D
1平移到如图3所示的位置时,猜想图中的D
1E与D
2F的数量关系,并证明你的猜想;
(2)设平移距离D
2D
1为x,△AC
1D
1与△BC
2D
2重叠部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的x的值使得y=

S
△ABC;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:2012年吉林省白城市镇赉县中考数学模拟试卷(三)(解析版)
题型:解答题
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成△AC
1D
1和△BC
2D
2两个三角形(如图所示).将纸片△AC
1D
1沿直线D
2B(AB)方向平移(点A,D
1,D
2,B始终在同一直线上),当点D
1于点B重合时,停止平移.在平移过程中,C
1D
1与BC
2交于点E,AC
1与C
2D
2、BC
2分别交于点F、P.
(1)当△AC
1D
1平移到如图3所示的位置时,猜想图中的D
1E与D
2F的数量关系,并证明你的猜想;
(2)设平移距离D
2D
1为x,△AC
1D
1与△BC
2D
2重叠部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的x的值使得y=

S
△ABC;若不存在,请说明理由.

查看答案和解析>>
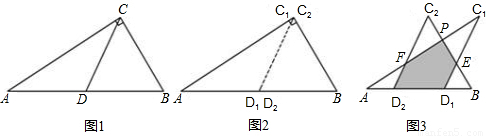
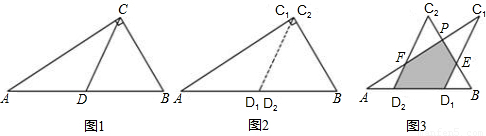
科目:czsx
来源:
题型:
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成△AC
1D
1和△BC
2D
2两个三角形(如图2所示).将纸片△AC
1D
1沿直线D
2B(AB)方向平移(点A,D
1,D
2,B始终在同一直线上),当点D
1与点B重合时,停止平移.在平移的过程中,C
1D
1与BC
2交于点E,AC
1与C
2D
2、BC
2分别交于点F、P.
【小题1】当△AC
1D
1平移到如图3所示位置时,猜想D
1E与D
2F的数量关系,并说明理由
【小题2】设平移距离D
2D
1为x,△AC
1D
1和△BC
2D
2重复部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
【小题3】对于(2)中的结论是否存在这样的x,使得重复部分面积等于原△ABC纸片面积的
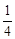
?若存在,请求出x的值;若不存在,请说明理由.
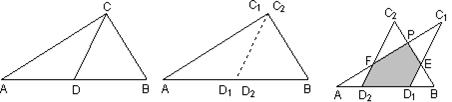
图1 图2 图3
查看答案和解析>>
科目:czsx
来源:第27章《二次函数》常考题集(24):27.3 实践与探索(解析版)
题型:解答题
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成△AC
1D
1和△BC
2D
2两个三角形(如图所示).将纸片△AC
1D
1沿直线D
2B(AB)方向平移(点A,D
1,D
2,B始终在同一直线上),当点D
1于点B重合时,停止平移.在平移过程中,C
1D
1与BC
2交于点E,AC
1与C
2D
2、BC
2分别交于点F、P.
(1)当△AC
1D
1平移到如图3所示的位置时,猜想图中的D
1E与D
2F的数量关系,并证明你的猜想;
(2)设平移距离D
2D
1为x,△AC
1D
1与△BC
2D
2重叠部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的x的值使得y=

S
△ABC;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:2006年重庆市中考数学试卷(综合卷)(解析版)
题型:解答题
(2006•重庆)如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成△AC
1D
1和△BC
2D
2两个三角形(如图所示).将纸片△AC
1D
1沿直线D
2B(AB)方向平移(点A,D
1,D
2,B始终在同一直线上),当点D
1于点B重合时,停止平移.在平移过程中,C
1D
1与BC
2交于点E,AC
1与C
2D
2、BC
2分别交于点F、P.
(1)当△AC
1D
1平移到如图3所示的位置时,猜想图中的D
1E与D
2F的数量关系,并证明你的猜想;
(2)设平移距离D
2D
1为x,△AC
1D
1与△BC
2D
2重叠部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的x的值使得y=

S
△ABC;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:第23章《二次函数与反比例函数》常考题集(23):23.5 二次函数的应用(解析版)
题型:解答题
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成△AC
1D
1和△BC
2D
2两个三角形(如图所示).将纸片△AC
1D
1沿直线D
2B(AB)方向平移(点A,D
1,D
2,B始终在同一直线上),当点D
1于点B重合时,停止平移.在平移过程中,C
1D
1与BC
2交于点E,AC
1与C
2D
2、BC
2分别交于点F、P.
(1)当△AC
1D
1平移到如图3所示的位置时,猜想图中的D
1E与D
2F的数量关系,并证明你的猜想;
(2)设平移距离D
2D
1为x,△AC
1D
1与△BC
2D
2重叠部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的x的值使得y=

S
△ABC;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:2012年贵州省中考数学模拟试卷(六)(解析版)
题型:解答题
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成△AC
1D
1和△BC
2D
2两个三角形(如图所示).将纸片△AC
1D
1沿直线D
2B(AB)方向平移(点A,D
1,D
2,B始终在同一直线上),当点D
1于点B重合时,停止平移.在平移过程中,C
1D
1与BC
2交于点E,AC
1与C
2D
2、BC
2分别交于点F、P.
(1)当△AC
1D
1平移到如图3所示的位置时,猜想图中的D
1E与D
2F的数量关系,并证明你的猜想;
(2)设平移距离D
2D
1为x,△AC
1D
1与△BC
2D
2重叠部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的x的值使得y=

S
△ABC;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:2013年天津市中考数学模拟试卷(一)(解析版)
题型:解答题
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成△AC
1D
1和△BC
2D
2两个三角形(如图所示).将纸片△AC
1D
1沿直线D
2B(AB)方向平移(点A,D
1,D
2,B始终在同一直线上),当点D
1于点B重合时,停止平移.在平移过程中,C
1D
1与BC
2交于点E,AC
1与C
2D
2、BC
2分别交于点F、P.
(1)当△AC
1D
1平移到如图3所示的位置时,猜想图中的D
1E与D
2F的数量关系,并证明你的猜想;
(2)设平移距离D
2D
1为x,△AC
1D
1与△BC
2D
2重叠部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的x的值使得y=

S
△ABC;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:2012年山东省青岛市中考数学一模试卷(解析版)
题型:解答题
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成△AC
1D
1和△BC
2D
2两个三角形(如图所示).将纸片△AC
1D
1沿直线D
2B(AB)方向平移(点A,D
1,D
2,B始终在同一直线上),当点D
1于点B重合时,停止平移.在平移过程中,C
1D
1与BC
2交于点E,AC
1与C
2D
2、BC
2分别交于点F、P.
(1)当△AC
1D
1平移到如图3所示的位置时,猜想图中的D
1E与D
2F的数量关系,并证明你的猜想;
(2)设平移距离D
2D
1为x,△AC
1D
1与△BC
2D
2重叠部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的x的值使得y=

S
△ABC;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:2013年山东省泰安市中考数学模拟试卷(十三)(解析版)
题型:解答题
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成△AC
1D
1和△BC
2D
2两个三角形(如图所示).将纸片△AC
1D
1沿直线D
2B(AB)方向平移(点A,D
1,D
2,B始终在同一直线上),当点D
1于点B重合时,停止平移.在平移过程中,C
1D
1与BC
2交于点E,AC
1与C
2D
2、BC
2分别交于点F、P.
(1)当△AC
1D
1平移到如图3所示的位置时,猜想图中的D
1E与D
2F的数量关系,并证明你的猜想;
(2)设平移距离D
2D
1为x,△AC
1D
1与△BC
2D
2重叠部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的x的值使得y=

S
△ABC;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2012年中考数学综合练习卷(解析版)
题型:解答题
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成△AC
1D
1和△BC
2D
2两个三角形(如图所示).将纸片△AC
1D
1沿直线D
2B(AB)方向平移(点A,D
1,D
2,B始终在同一直线上),当点D
1于点B重合时,停止平移.在平移过程中,C
1D
1与BC
2交于点E,AC
1与C
2D
2、BC
2分别交于点F、P.
(1)当△AC
1D
1平移到如图3所示的位置时,猜想图中的D
1E与D
2F的数量关系,并证明你的猜想;
(2)设平移距离D
2D
1为x,△AC
1D
1与△BC
2D
2重叠部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的x的值使得y=

S
△ABC;若不存在,请说明理由.

查看答案和解析>>





 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.
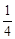 ?若存在,请求出x的值;若不存在,请说明理由.
?若存在,请求出x的值;若不存在,请说明理由.
 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.

 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.
 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.
 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.
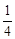 ?若存在,请求出x的值;若不存在,请说明理由.
?若存在,请求出x的值;若不存在,请说明理由.
 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.
 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.
 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.
 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.
 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.
 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.
 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.
 S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.