精英家教网 >
试题搜索列表 >已知数列an,a1=1,a2=-2,a(n+2)=-1/a(n),求前26项的和
已知数列an,a1=1,a2=-2,a(n+2)=-1/a(n),求前26项的和答案解析
科目:gzsx
来源:
题型:
已知数列a
n满足
a1=1,an+1=(1+cos2)an+sin2,n∈N*.
(1)求a
2,a
3,a
4;并求证:a
2m+1+2=2(a
2m-1+2),(m∈N
*);
(2)设
bn=,Sn=b1+b2+…+bn,求证:
Sn<n+.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知数列a
n满足a
1=1,n≥2时,
=.
(1)求证:数列
{}为等差数列;
(2)求
{}的前n项和.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知数列a
n中a
1=1,点P(a
n,a
n+1)在直线y=x+2上,
(1)求数列a
n的通项公式;
(2)设
Sn=++…+,求S
n.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知数列a
n满足a
1=1,a
n+1=a
n+n(n∈N
*),数列b
n满足b
1=1,(n+2)b
n+1=nb
n(n∈N
*),数列c
n满足
c1=1,++…+=(n∈N
*)
(1)求数列{a
n}、{b
n}的通项公式;
(2)求数列c
n的通项公式;
(3)是否存在正整数k使得
k(an+)->cn+6n+15对一切n∈N
*恒成立,若存在求k的最小值;若不存在请说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:

18、已知数列a
n,a
1=1,a
n+1=a
n+2n,计算数列a
n的第20项.现已给出该问题算法的流程图(如图所示).
(Ⅰ)请在图中判断框中的(A)与执行框中的(B)处填上合适的语句,使之能完成该题的算法功能.
(Ⅱ) 根据流程图写出程序语句.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知数列an满足a1=1,且4an+1-anan+1+2an=9(n∈N*)
(1)求a1,a2,a3,a4的值;
(2)由(1)猜想an的通项公式,并给出证明.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
已知数列an满足a1=1,且4an+1-anan+1+2an=9(n∈N*)
(1)求a1,a2,a3,a4的值;
(2)由(1)猜想an的通项公式,并给出证明.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
已知数列an满足a1=1,an+1=an+n(n∈N*),数列bn满足b1=1,(n+2)bn+1=nbn(n∈N*),数列cn满足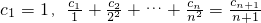 (n∈N*)
(n∈N*)
(1)求数列an、bn的通项公式;
(2)求数列cn的通项公式;
(3)是否存在正整数k使得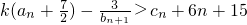 对一切n∈N*恒成立,若存在求k的最小值;若不存在请说明理由.
对一切n∈N*恒成立,若存在求k的最小值;若不存在请说明理由.
查看答案和解析>>
科目:gzsx
来源:2010年北京大学附中高考数学考前猜题试卷(解析版)
题型:解答题
已知数列an满足a1=1,且4an+1-anan+1+2an=9(n∈N*)
(1)求a1,a2,a3,a4的值;
(2)由(1)猜想an的通项公式,并给出证明.
查看答案和解析>>
科目:gzsx
来源:2010-2011学年广东省梅州市梅州中学高二(上)期末数学试卷(理科)(解析版)
题型:解答题
已知数列a
n中a
1=1,点P(a
n,a
n+1)在直线y=x+2上,
(1)求数列a
n的通项公式;
(2)设

,求S
n.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
已知数列an满足a1=1,n≥2时,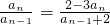 .
.
(1)求证:数列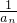 为等差数列;
为等差数列;
(2)求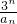 的前n项和.
的前n项和.
查看答案和解析>>
科目:gzsx
来源:2008-2009学年河北省衡水中学高一(下)第二次调研数学试卷(必修2)(解析版)
题型:解答题
已知数列a
n满足a
1=1,n≥2时,
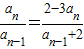
.
(1)求证:数列

为等差数列;
(2)求

的前n项和.
查看答案和解析>>
科目:gzsx
来源:2010-2011学年湖北省安陆一中高二(上)期末数学综合测试卷(必修3)(解析版)
题型:解答题

已知数列a
n,a
1=1,a
n+1=a
n+2n,计算数列a
n的第20项.现已给出该问题算法的流程图(如图所示).
(Ⅰ)请在图中判断框中的(A)与执行框中的(B)处填上合适的语句,使之能完成该题的算法功能.
(Ⅱ) 根据流程图写出程序语句.
查看答案和解析>>
科目:gzsx
来源:不详
题型:解答题
已知数列a
n满足a
1=1,a
n+1=a
n+n(n∈N
*),数列b
n满足b
1=1,(n+2)b
n+1=nb
n(n∈N
*),数列c
n满足
c1=1,++…+=(n∈N
*)
(1)求数列a
n、b
n的通项公式;
(2)求数列c
n的通项公式;
(3)是否存在正整数k使得
k(an+)->cn+6n+15对一切n∈N
*恒成立,若存在求k的最小值;若不存在请说明理由.
查看答案和解析>>
科目:gzsx
来源:不详
题型:解答题
已知数列an满足a1=1,且4an+1-anan+1+2an=9(n∈N*)
(1)求a1,a2,a3,a4的值;
(2)由(1)猜想an的通项公式,并给出证明.
查看答案和解析>>
科目:gzsx
来源:2011年江苏省高考数学预测试卷(3)(解析版)
题型:解答题
已知数列an满足a1=1,且4an+1-anan+1+2an=9(n∈N*)
(1)求a1,a2,a3,a4的值;
(2)由(1)猜想an的通项公式,并给出证明.
查看答案和解析>>
科目:gzsx
来源:2008-2009学年江苏省泰州市实验中学高一(下)期中数学试卷(解析版)
题型:解答题
已知数列a
n满足a
1=1,a
n+1=a
n+n(n∈N
*),数列b
n满足b
1=1,(n+2)b
n+1=nb
n(n∈N
*),数列c
n满足

(n∈N
*)
(1)求数列a
n、b
n的通项公式;
(2)求数列c
n的通项公式;
(3)是否存在正整数k使得

对一切n∈N
*恒成立,若存在求k的最小值;若不存在请说明理由.
查看答案和解析>>
科目:gzsx
来源:2011年高考数学附加题部分专项训练2(理科)(解析版)
题型:解答题
已知数列an满足a1=1,且4an+1-anan+1+2an=9(n∈N*)
(1)求a1,a2,a3,a4的值;
(2)由(1)猜想an的通项公式,并给出证明.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
已知数列an中a1=1,点P(an,an+1)在直线y=x+2上,
(1)求数列an的通项公式;
(2)设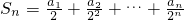 ,求Sn.
,求Sn.
查看答案和解析>>
科目:gzsx
来源:不详
题型:解答题
已知数列a
n满足a
1=1,n≥2时,
=.
(1)求证:数列
{}为等差数列;
(2)求
{}的前n项和.
查看答案和解析>>

 18、已知数列an,a1=1,an+1=an+2n,计算数列an的第20项.现已给出该问题算法的流程图(如图所示).
18、已知数列an,a1=1,an+1=an+2n,计算数列an的第20项.现已给出该问题算法的流程图(如图所示).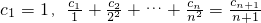 (n∈N*)
(n∈N*)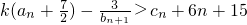 对一切n∈N*恒成立,若存在求k的最小值;若不存在请说明理由.
对一切n∈N*恒成立,若存在求k的最小值;若不存在请说明理由. ,求Sn.
,求Sn.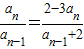 .
. 为等差数列;
为等差数列; 的前n项和.
的前n项和. 已知数列an,a1=1,an+1=an+2n,计算数列an的第20项.现已给出该问题算法的流程图(如图所示).
已知数列an,a1=1,an+1=an+2n,计算数列an的第20项.现已给出该问题算法的流程图(如图所示). (n∈N*)
(n∈N*) 对一切n∈N*恒成立,若存在求k的最小值;若不存在请说明理由.
对一切n∈N*恒成立,若存在求k的最小值;若不存在请说明理由.