练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >单规定圆心的依据

    单规定圆心的依据答案解析

    科目：czsx 来源： 题型：

    用尺规作一个角的角平分线的示意图如下，作法是：以O为圆心作一圆弧交角的两边于A、B两点；再分别以A、B两点为圆心，以大于
    1
    2
    AB的相同的长度为半径作两条圆弧；两条圆弧相交于P点，则OP就是∠AO的角平分线．由作法可知，判断△OAP≌△OBP的依据是（　　）

    查看答案和解析>>

    科目：czsx 来源： 题型：阅读理解

    阅读下列材料（共9分）
    1872年，新政府宣布停止使用以月亮运行为基础的历法（太阴历），而同西洋各国一样，明确实行以太阳的运行为基础的太阳历。而且确定一天为24小时，一周为7天，将此作为全国的共同时间。于是，人们生活所依据的历法和时间的划分发生了很大的变化。
    此前，普通民众一年中的重大节日（如3月3日，5月5日，7月7日等），都是从中国传入的。政府改以天皇和皇室的活动为中心，规定新的节日，要求民众届时庆祝。如神武天皇即位日（神话传说中的第一位天皇），天皇的生日等。
    但是，由于旧历法及基于旧历法的各种节日活动同农业生产及习俗密切关联，所以在有些地域仍然长时间地延续着。
    ——《东亚三国的近现代史》
    请回答：
    （1）结合所学知识，简述日本改变历法的原因。（2分）
    （2）概括日本节日改革的特点，并简要分析出现这种特点的原因。（4分）
    （3）结合材料和所学知识，分析日本历法和节日改革的效果。（3分）

    查看答案和解析>>

    科目：czsx 来源： 题型：

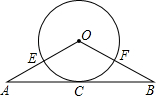    精英家教网如图，△ABO中，OA=OB，以O为圆心的圆经过AB中点C，且分别交OA、OB于点E、F．
    （1）求证：AB是⊙O切线；
    （2）若∠B=30°，且AB=4
    		3
    ，求
    ECF
    的长（结果保留π）

    查看答案和解析>>

    科目：czsx 来源： 题型：阅读理解

    25、在一次数学单元测验中，老师发现小敏同学有一道题只完成了一步，其解答是正确的，遗憾的是她没有做完整．现请你阅读这道题，并完成下列问题：
    （1）在她已完成这步后面的括号里填上适当的依据．
    （2）请你继续完成他未解答的说理过程．
    这道题的题目是：
    如图，己知EF∥BC，∠1=∠B，问DF与AB平行吗？请说明理由．
    答：DF与AB平行，理由：
    ∵EF∥BC
    ∴∠2=∠B（
    两直线平行，同位角相等
    ）

    查看答案和解析>>

    科目：czsx 来源： 题型：

    用直尺和圆规作一个角等于已知角的示意图如下，则要说明∠D′O′C′=∠DOC，需要证明△D′O′C′≌△DOC，则这两个三角形全等的依据是（　　）

    查看答案和解析>>

    科目：czsx 来源： 题型：

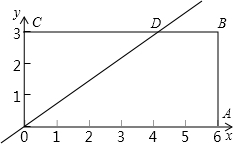    精英家教网如图，点P在双曲线y=
    4x
    上，以P为圆心的⊙P与两坐标轴都相切，E为y轴负半轴上的一点，PF⊥PE交x轴于点F，则OF-OE的值是
     
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    31、圆的两条平行弦与圆心的距离分别为3和4，则此二平行弦之间的距离为
    1cm或7cm
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    精英家教网在生活中，我们常常会看到如图所示的情况，在电线杆上拉两根钢筋来加固电线杆，这样做的依据是
     
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    矩形OABC在直角坐标系中的位置如图所示，A、C两点的坐标分别为A（6，0）、C（0，3），直线y=
    34
    x    与BC边相交于点D．
    （1）若抛物线y=ax2+bx（a≠0）经过D、A两点，试确定此抛物线的表达式；
    （2）若以点A为圆心的⊙A与直线OD相切，试求⊙A的半径；
    （3）设（1）中抛物线的对称轴与直线OD交于点M，在对称轴上是否存在点精英家教网Q，以Q、O、M为顶点的三角形与△OCD相似？若存在，试求出符合条件的Q点的坐标；若不存在，试说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：

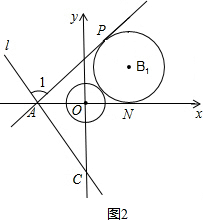
    如图，在以O为圆心的两个同心圆中，小圆的半径长为2，大圆的弦AB与小圆交于点精英家教网C、D，且AB=3CD，∠COD=60°．
    （1）求大圆半径的长；
    （2）若大圆的弦AE与小圆切于点F，求AE的长．

    查看答案和解析>>

    科目：czsx 来源： 题型：

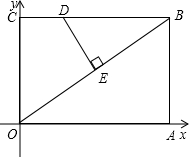    如图在平面直角坐标系中，矩形OABC的边OC=6，对角线OB所在直线的函数解析式精英家教网为y=
    34
    x    ．
    （1）直接写出C点的坐标；
    （2）若D是BC边上的点，过D作DE⊥OB于E，已知DE=3.6．
    ①求出CD的长；
    ②以点C为圆心，CD长为半径作⊙C、试问在对角线OB上是否存在点P，使得以点P为圆心的⊙P与⊙C、x轴都相切？若存在，求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如图1，在平面直角坐标系中，以坐标原点O为圆心的⊙O的半径为
    		2
    -1    ，直线l：y=-x-
    		2
    与坐标轴分别交于A、C两点，点B的坐标为（4，1），⊙B与x轴相切于点M．
    （1）求点A的坐标及∠CAO的度数；
    （2）⊙B以每秒1个单位长度的速度沿x轴负方向平移，同时，若直线l绕点A顺时针匀速旋转，当⊙B第一次与⊙O相切时，直线l也恰好与⊙B第一次相切，见图（2）求B1的坐标以及直线AC绕点A每秒旋转多少度？
    （3）若直线l不动，⊙B沿x轴负方向平移过程中，能否与⊙O与直线l同时相切？若相切，说明理由．
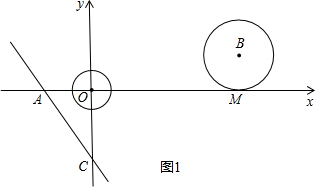
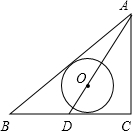    精英家教网精英家教网

    查看答案和解析>>

    科目：czsx 来源： 题型：

    分式的基本性质是进行分式化简和运算的依据，用公式表示分式的基本性质：
    b
    a
    =
    bc
    ac
    （c≠0）
    b
    a
    =
    bc
    ac
    （c≠0）
    ，
    b
    a
    =
    b÷c
    a÷c
    （c≠0）
    b
    a
    =
    b÷c
    a÷c
    （c≠0）
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    定义新运算：规定符号“*”的意义是a*b=
    ab
    a+b
    ，则[2*（-3）]*4的值为
    12
    5
    12
    5
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    在某段限速公路BC上（公路视为直线），交通管理部门规定汽车的最高行驶速度不能超过60千米/时 （即
    50
    3
    米/秒），并在离该公路100米处设置了一个监测点A．在如图所示的直角坐标系中，点A位于y轴上，测速路段BC在x轴上，点B在A的北偏西60°方向上，点C在A的北偏东45°方向上，另外一条高速公路在y轴上，AO为其中的一段．精英家教网
    （1）写出A、B、C三点的坐标；
    （2）一辆汽车从点B匀速行驶到点C所用的时间是15秒，通过计算，判断该汽车在这段限速路上是否超速？（参考数据：
    		3
    ≈1.7    ）
    （3）若一辆大货车在限速路上以60千米/时的速度由C处向西行驶，同时一辆小汽车在高速公路上由A处以货车2倍的速度向北行驶，求两车在匀速行驶半分钟后，它们的距离是多少米？（结果保留根号）

    查看答案和解析>>

    科目：czsx 来源： 题型：

    精英家教网如图△ABC中，∠C=90°，AC=6，AB=10，D是BC边的中点，以AD上一点O为圆心的圆与AB，BC都相切，则⊙O的半径为（　　）
    A、
    12
    7
    B、
    1
    5
    C、
    5
    3
    D、2

    查看答案和解析>>

    科目：czsx 来源： 题型：

    16、下列命题中正确的是（　　）

    查看答案和解析>>

    科目：czsx 来源： 题型：

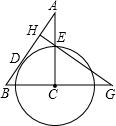    精英家教网如图，在△ABC中，∠A=90°，分别以B、C为圆心的两个等圆外切，两圆的半径都为2cm，则图中阴影部分的面积为
     
    cm2．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    精英家教网如图，在△ABC中，∠ACB=90°，以C为圆心的圆切AB于点D，交AC于点E，过点E作AB的垂线，垂足为H，HE交BC的延长线于点G，已知∠A=α，AE=m，则EG=
     
    （用含α，m的式子表示）．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    精英家教网如图，以O为圆心的两个同心圆中，大圆的弦AB切小圆于P，如果AB=4cm，则图中阴影部分的面积为
     
    cm2．（结果用π表示）

    查看答案和解析>>