练习册

  • 练习册
  • 试题
    设x1＜x2＜-xn.nN且n≥2.若{x|(x-x2)(x-x3)-(x-xn)＞0}{x|x2-(x1+xn)x+x1xn＞0}.则n ( ) (A)等于2 (B)是大于2的任意奇数 (C)是大于2的任意偶数 (D)是大于1的任意自然数 【查看更多】

     

    题目列表(包括答案和解析)

    设f（x）的定义域为（0，+∞），f（x）的导函数为f'（x），且对任意正数x均有f′(x)＞
    f(x)
    x
    ，
    （1）判断函数F(x)=
    f(x)
    x
    在（0，+∞）上的单调性；
    （2）设x1，x2∈（0，+∞），比较f（x1）+f（x2）与f（x1+x2）的大小，并证明你的结论；
    （3）设x1，x2，…xn∈（0，+∞），若n≥2，比较f（x1）+f（x2）+…+f（xn）与f（x1+x2+…+xn）的大小，并证明你的结论．

    查看答案和解析>>

    设x1，x2…，xn∈R+，求证：
    x12
    x2
    +
    x22
    x3
    +…+
    xn-12
    xn
    +
    x
    2
    n
    x1
    ≥x1+x2+…+xn．

    查看答案和解析>>

    设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线,如图所示,以下结论中正确的是…(　　)

    A.x和y的相关系数为直线l的斜率

    B.x和y的相关系数在0到1之间

    C.当n为偶数时,分布在l两侧的样本点的个数一定相同

    D.直线l过点()

    查看答案和解析>>

    设f（x）的定义域为（0，+∞），f（x）的导函数为f'（x），且对任意正数x均有数学公式，
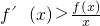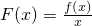    （1）判断函数数学公式在（0，+∞）上的单调性；
    （2）设x1，x2∈（0，+∞），比较f（x1）+f（x2）与f（x1+x2）的大小，并证明你的结论；
    （3）设x1，x2，…xn∈（0，+∞），若n≥2，比较f（x1）+f（x2）+…+f（xn）与f（x1+x2+…+xn）的大小，并证明你的结论．

    查看答案和解析>>

    设f（x）的定义域为（0，+∞），f（x）的导函数为f'（x），且对任意正数x均有，
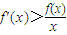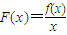    （1）判断函数在（0，+∞）上的单调性；
    （2）设x1，x2∈（0，+∞），比较f（x1）+f（x2）与f（x1+x2）的大小，并证明你的结论；
    （3）设x1，x2，…xn∈（0，+∞），若n≥2，比较f（x1）+f（x2）+…+f（xn）与f（x1+x2+…+xn）的大小，并证明你的结论．

    查看答案和解析>>


    同步练习册答案