解:(1)由于
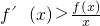
得,
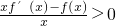
,而x>0,
则xf′(x)-f(x)>0,
则F′(x)=
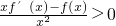
,因此
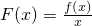
在(0,+∞)上是增函数.
(2)由于x
1,x
2∈(0,+∞),则0<x
1<x
1+x
2,而
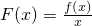
在(0,+∞)上是增函数,则F(x
1)<F(x
1+x
2),即
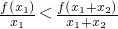
,
∴(x
1+x
2)f(x
1)<x
1f(x
1+x
2)(1),同理 (x
1+x
2)f(x
2)<x
2f(x
1+x
2)(2)
(1)+(2)得:(x
1+x
2)[f(x
1)+f(x
2)]<(x
1+x
2)f(x
1+x
2),而x
1+x
2>0,
因此 f(x
1)+f(x
2)<f(x
1+x
2).
(3)证法1:由于x
1,x
2∈(0,+∞),则0<x
1<x
1+x
2+…+x
n,而
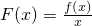
在(0,+∞)上是增函数,则F(x
1)<F(x
1+x
2+…+x
n),
即
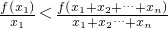
,
∴(x
1+x
2+…+x
n)f(x
1)>x
1f(x
1+x
2+…+x
n)
同理 (x
1+x
2+…+x
n)f(x
2)>x
2f(x
1+x
2+…+x
n)…(x
1+x
2+…+x
n)f(x
n)>x
nf(x
1+x
2+…+x
n)
以上n个不等式相加得:(x
1+x
2+…+x
n)[f(x
1)+f(x
2)+…f(x
n)]>(x
1+x
2+…+x
n)f(x
1+x
2+…+x
n)
而x
1+x
2+…+x
n>0,f(x
1)+f(x
2)+…f(x
n)>f(x
1+x
2+…+x
n).
证法2:数学归纳法
①当n=2时,由(2)知,不等式成立;
②当n=k(n≥2)时,不等式f(x
1)+f(x
2)+…f(x
n)>f(x
1+x
2+…+x
n)成立,
即f(x
1)+f(x
2)+…f(x
k)>f(x
1+x
2+…+x
k)成立,
则当n=k+1时,f(x
1)+f(x
2)+…f(x
k)+f(x
k+1)>f(x
1+x
2+…+x
k)+f(x
k+1)
再由(2)的结论,f(x
1+x
2+…+x
k)+f(x
k+1)>f[(x
1+x
2+…+x
k)+x
k+1]f(x
1+x
2+…+x
k)+f(x
k+1)>f(x
1+x
2+…+x
k+x
k+1)
因此不等式f(x
1)+f(x
2)+…f(x
n)>f(x
1+x
2+…+x
n)对任意n≥2的自然数均成立
分析:(1)通过
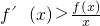
推出
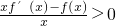
,说明F′(x)=
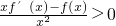
,即可得到
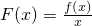
在(0,+∞)上是增函数.
(2)设x
1,x
2∈(0,+∞),0<x
1<x
1+x
2,而
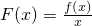
在(0,+∞)上是增函数,推出
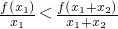
,
然后推出 f(x
1)+f(x
2)<f(x
1+x
2).即可.
(3)法一:类似(2)的方法通过函数的单调性证明:设
1,x
2,…x
n∈(0,+∞),f(x
1)+f(x
2)+…f(x
n)>f(x
1+x
2+…+x
n)
法二:利用数学归纳法,利用(2)的验证n=2时猜想成立,然后假设n=k时猜想成立,然后证明n=k+1时猜想也成立即可.
点评:本题考查函数的单调性,函数值的大小比较,单调性的应用,数学归纳法的应用,注意数学归纳法的证明必须用上假设,考查逻辑推理能力,转化思想.

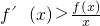 ,
,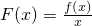 在(0,+∞)上的单调性;
在(0,+∞)上的单调性;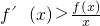 得,
得,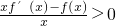 ,而x>0,
,而x>0,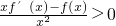 ,因此
,因此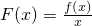 在(0,+∞)上是增函数.
在(0,+∞)上是增函数.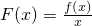 在(0,+∞)上是增函数,则F(x1)<F(x1+x2),即
在(0,+∞)上是增函数,则F(x1)<F(x1+x2),即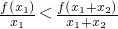 ,
,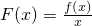 在(0,+∞)上是增函数,则F(x1)<F(x1+x2+…+xn),
在(0,+∞)上是增函数,则F(x1)<F(x1+x2+…+xn),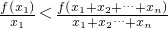 ,
,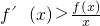 推出
推出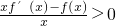 ,说明F′(x)=
,说明F′(x)=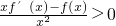 ,即可得到
,即可得到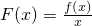 在(0,+∞)上是增函数.
在(0,+∞)上是增函数.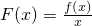 在(0,+∞)上是增函数,推出
在(0,+∞)上是增函数,推出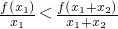 ,
,

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案