
题目列表(包括答案和解析)
三、解答题 :(本大题共5小题,每小题12分,共60分。解答应写出证明过程或演算步骤)
19.(本小题满分12分)
对某校110个小学生进行心理障碍测试得到如下的列联表:
|
|
焦虑 |
说谎 |
懒惰 |
总计 |
|
女生 |
5 |
10 |
15 |
30 |
|
男生 |
20 |
10 |
50 |
80 |
|
总计 |
25 |
20 |
65 |
110 |
通过计算说明在这三种心理障碍中哪一种与性别关系最大?
解答题
某公司取消福利分房和公费医疗,实行年薪制工资结构改革,该公司从2000年起,每人的工资由三个项目组成,并按下表规定实施:
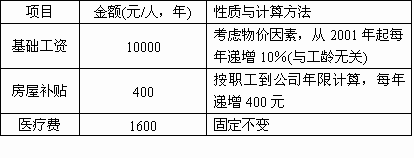
如果该公司今年有5位职工,计划从明年起每年招5名职工.
(1)若2000年算第一年,试把第n年该公司付给职工工资总额y(万元)表示成年限n的函数;
(2)试判断公司第n年发给职工工资总额中,房屋补贴和医疗费的总和能否超过基础工资总额的20%.
某集团准备投资1200万元兴办一所完全中学(包括初中和高中),为了考虑社会效益和经济效益,对该地区教育市场进行调查,得出一组数据列表(以班为单位)如下:

根据物价部门的规定:初中是义务教育阶段,收费标准适当控制,预计除书本费、公办费以外,每生每年可收取600元;高中每生每年可收取1500元.因生源和环境等条件限制,办学规模以20至30个班为宜,教师实行聘任制,初、高中的教育周期均为三年.请你合理安排招生计划,使得年利润最大.照这样计算,大约经过多少年可收回全部投资?
| |||||||||||
|
|
|
|
| 5 |
| 5 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com