
题目列表(包括答案和解析)
(1)已知cosα=-![]() ,且α为第三象限角,求sinα的值
,且α为第三象限角,求sinα的值
(2)已知tanα=3,计算![]() 的值
的值
(1)已知cosα=-![]() ,且α为第三象限角,求sinα的值
,且α为第三象限角,求sinα的值
(2)已知tanα=3,计算![]() 的值
的值
已知cosα=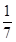 ,cos(α-β)=
,cos(α-β)=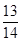 ,且0<β<α<
,且0<β<α<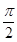 .
.
(1)求tan2α的值;
(2)求β的值.
(本小题满分12分) 已知cosα=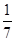 ,cos(α-β)=
,cos(α-β)=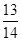 ,且0<β<α<
,且0<β<α< 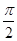 .
.
(1)求tan2α的值;
(2)求β
(1)①证明:两角和的余弦公式C(α+β):cos(α+β)=cos αcos β-sin αsin β;
②由C(α+β)推导两角和的正弦公式S(α+β):sin(α+β)=sin αcos β+cos αsin β.
(2)已知cos α=-![]() ,α∈(π,
,α∈(π,![]() π),
π),![]() tan β=-
tan β=-![]() ,β∈(
,β∈(![]() ,π),求cos(α+β).
,π),求cos(α+β).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com