
题目列表(包括答案和解析)
 如图是一幅招贴画的示意图,其中ABCD是边长为2a的正方形,周围是四个全等的弓形.已知O为正方形的中心,G为AD的中点,点P在直线OG上,弧AD是以P为圆心、PA为半径的圆的一部分,OG的延长线交弧AD于点H.设弧AD的长为l,∠APH=θ,θ∈(
如图是一幅招贴画的示意图,其中ABCD是边长为2a的正方形,周围是四个全等的弓形.已知O为正方形的中心,G为AD的中点,点P在直线OG上,弧AD是以P为圆心、PA为半径的圆的一部分,OG的延长线交弧AD于点H.设弧AD的长为l,∠APH=θ,θ∈(| π |
| 4 |
| 3π |
| 4 |
| OP |
| l |
| π |
| 4 |
 (2013•枣庄二模)如图所示,墙上挂有边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的圆孤,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是
(2013•枣庄二模)如图所示,墙上挂有边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的圆孤,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是| π |
| 4 |
| π |
| 4 |
 (2013•枣庄二模)如图所示,墙上挂有一块边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的扇形.某人向此木板投镖,假设每次都能击中木板,且击中阴影部分的概率为
(2013•枣庄二模)如图所示,墙上挂有一块边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的扇形.某人向此木板投镖,假设每次都能击中木板,且击中阴影部分的概率为| π |
| 4 |
| π |
| 4 |
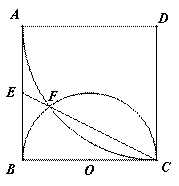
A.选修4-1(几何证明选讲)
如图,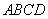 是边长为
是边长为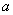 的正方形,以
的正方形,以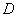 为圆心,
为圆心,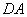 为半径的圆弧与以
为半径的圆弧与以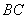 为直径的
为直径的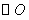 交于点
交于点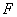 ,延长
,延长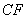 交
交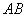 于
于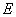 .(1)求证:
.(1)求证: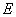 是
是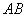 的中点;(2)求线段
的中点;(2)求线段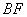 的长.
的长.
B.选修4-2(矩阵与变换)
已知矩阵 ,若矩阵
,若矩阵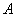 属于特征值3的一个特征向量为
属于特征值3的一个特征向量为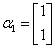 ,属于特征值-1的一个特征向量为
,属于特征值-1的一个特征向量为 ,求矩阵
,求矩阵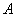 .
.
C.选修4-4(坐标系与参数方程)
在极坐标系中,曲线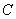 的极坐标方程为
的极坐标方程为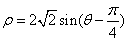 ,以极点为原点,极轴为
,以极点为原点,极轴为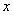 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线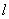 的参数方程为
的参数方程为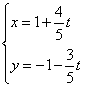 (
(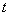 为参数),求直线
为参数),求直线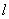 被曲线
被曲线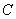 所截得的弦长.
所截得的弦长.
D.选修4—5(不等式选讲)
已知实数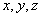 满足
满足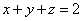 ,求
,求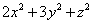 的最小值;
的最小值;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com