
题目列表(包括答案和解析)
5.过双曲线x2-y2=8的左焦点F1有一条弦PQ在左支上,若|PQ|=7,F2是双曲线的右焦点,则△PF2Q的周长是( )
A.28 B.14-8
C.14+8 D.8
解析:|PF2|+|PQ|+|QF2|
=|PF2|-|PF1|+|QF2|-|QF1|+2·|PQ|
=14+8.
答案:C
4.我们把离心率为e=的双曲线-=1(a>0,b>0)称为黄金双曲线.给出以下几个说法:
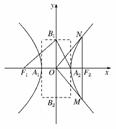
①双曲线x2-=1是黄金双曲线;
②若b2=ac,则该双曲线是黄金双曲线;
③若∠F1B1A2=90°,则该双曲线是黄金双曲线;
④若∠MON=90°,则该双曲线是黄金双曲线.
其中正确的是( )
A.①② B.①③
C.①③④ D.①②③④
解析:①e====,双曲线是黄金双曲线.
②由b2=ac,可得c2-a2=ac,两边同除以a2,即e2-e-1=0,从而e=,双曲线是黄金双曲线.
③|F1B1|2=b2+c2,|A2B1|2=b2+a2,|F1A2|2=(a+c)2,注意到∠F1B1A2=90°,所以b2+c2+b2+a2=(a+c)2,即b2=ac,由②可知双曲线为黄金双曲线.
④∵|MN|=,由射影定理知|OF2|2=|MF2|·|F2N|,即c2=,从而b2=ac,由②可知双曲线为黄金双曲线.
答案:D
3.已知双曲线的两个焦点为F1(-,0)、F2(,0),M是此双曲线上的一点,且满足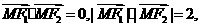 则该双曲线的方程是( )
则该双曲线的方程是( )
A.-y2=1 B.x2-=1
C.-=1 D.-=1
解析:设双曲线方程为-=1,且M为右支上一点,
由已知|MF1|-|MF2|=2a,
∴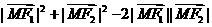 =4a2.
=4a2.
又∵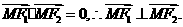
∴4c2-4=4a2,即b2=1.
又∵c=,∴a2=9.
∴双曲线方程为-y2=1,故选A.
答案:A
2.已知双曲线9y2-m2x2=1(m>0)的一个顶点到它的一条渐近线的距离为,则m等于( )
A.1 B.2
C.3 D.4
解析:9y2-m2x2=1(m>0)⇒a=,b=,取顶点,一条渐近线为mx-3y=0,
∵=⇒m2+9=25,
∴m=4,故选D.
答案:D
1.双曲线虚轴的一个端点为M,两个焦点为F1、F2,∠F1MF2=120°,则双曲线的离心率为( )
A. B.
C. D.
解析:由图易知:=tan60°=,
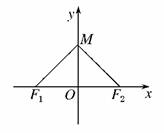
不妨设c=,b=1,则a=.
∴e===.故选B.
答案:B
13.(2010·福建)已知抛物线C:y2=2px(p>0)过点A(1,-2).
(1)求抛物线C的方程,并求其准线方程;
(2)是否存在平行于OA(O为坐标原点)的直线l,使得直线l与抛物线C有公共点,且直线OA与l的距离等于?若存在,求直线l的方程;若不存在,说明理由.
解:(1)将(1,-2)代入y2=2px,得(-2)2=2p·1,所以p=2.
故所求抛物线C的方程为y2=4x,其准线方程为x=-1.
(2)假设存在符合题意的直线l,其方程为y=-2x+t,
由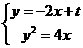 得y2+2y-2t=0.
得y2+2y-2t=0.
因为直线l与抛物线C有公共点,所以Δ=4+8t≥0,解得t≥-.
由直线OA与l的距离d=可得=,解得t=±1.
因为-1∉,1∈,
所以符合题意的直线l存在,其方程为2x+y-1=0.
12.是否存在同时满足下列条件的抛物线:①准线是y轴;②顶点在x轴上;③点A(3,0)到该抛物线上的动点P的距离的最小值为2?如果存在,求出抛物线方程;如果不存在,说明理由.
解:设满足条件的抛物线存在,顶点B在x轴上.
设B(a,0),以y轴为准线的抛物线方程为
y2=4a(x-a),由条件知a>0.
设P是抛物线上的点,其坐标为.
则|AP|2=2+m2
=[m2-12(a-a2)]2+12a-8a2,
∴当a-a2≥0,即0<a≤1,
且m2=12(a-a2)时,|AP|min=.
∴=2,解得a=1或a=.
此时抛物线方程为y2=4(x-1)或y2=2.
当a-a2<0,即a>1,且m=0时,
|AP|min=|a-3|=2.
∴a=5,此时抛物线方程为y2=20(x-5),
∴存在满足条件的抛物线,其方程为
y2=4(x-1)或y2=2或y2=20(x-5).
11.A、B是抛物线y2=2px(p>0)上的两点,且OA⊥OB.
(1)求A、B两点的横坐标之积和纵坐标之积;
(2)求证:直线AB过定点;
(3)求弦AB中点P的轨迹方程;
(4)求△AOB面积的最小值.
解:设A(x1,y1),B(x2,y2),中点P(x0,y0).
(1)kOA=,kOB=.
∵OA⊥OB,∴kOA·kOB=-1,∴x1x2+y1y2=0.
∵y=2px1,y=2px2,∴·+y1y2=0.
∵y1≠0,y2≠0,∴y1y2=-4p2,∴x1x2=4p2.
(2)∵y=2px1,y=2px2,
∴(y1-y2)(y1+y2)=2p(x1-x2).
∴=,∴kAB=.
∴直线AB:y-y1=(x-x1).
∴y=+y1-.
∴y=+.
∵y=2px1,y1y2=-4p2,∴y=+.
∴y=(x-2p).
∴AB过定点(2p,0).
(3)如图,设OA:y=kx,代入y2=2px得:x=0或x=,
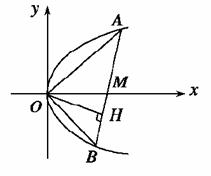
∴A.
同理,以-代k得B(2pk2,-2pk).
设中点坐标P(x0,y0),
∴.
∵k2+=2+2,∴=2+2,
即y=px0-2p2.
∴中点P的轨迹方程为y2=px-2p2.
(4)设M(2p,0),S△AOB=S△AOM+S△BOM=|OM|(|y1|+|y2|)=p(|y1|+|y2|)≥2p=4p2,当且仅当|y1|=|y2|=2p时,等号成立.
评析:解决直线与抛物线的有关问题时要注意以下几点:①设抛物线上的点为(x1,y1),(x2,y2);②因为(x1,y1),(x2,y2)都在抛物线上,故满足y=2px1,y=2px2;③利用yy=4p2x1x2可以整体得到y1y2或x1x2.
10.设x1、x2∈R,常数a>0,定义运算“*”:x1]x*a))的轨迹方程是________.
解析:由y=,得y2=x*a=(x+a)2-(x-a)2=4ax(y≥0).
答案:y2=4ax(y≥0)
9.已知F为抛物线C:y2=4x的焦点,过F且斜率为1的直线交C于A、B两点.设|FA|>|FB|,则|FA|与|FB|的比值等于________.
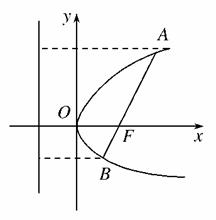
解析:抛物线C:y2=4x的焦点F(1,0),准线方程:x=-1,如图,
则直线AB的方程为y=x-1,
由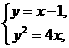 得
得
x2-6x+1=0,①
设A(x1,y1),B(x2,y2),则x1,x2是方程①的两根,
∴x1x2=1,x1=3+2.
根据抛物线定义,得|FA|=x1+1,
|FB|=x2+1(x1>x2),
∴====x1=3+2.
答案:3+2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com