
题目列表(包括答案和解析)
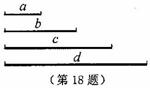
4. (2011浙江杭州, 18,6)四条线段a,b,c,d如图,a:b:c:d=1:2:3:4.
(1)选择其中的三条线段为边作一个三角形(尺规作图,要求保留作图痕迹,不必写出作法);
(2)任取三条线段,求以它们为边能作出三角形的概率.
[答案](1)只能取b,c,d三条线段,作图略
(2) 四条线段中任取三条共有四种等可性结果:(a,b,c),(a,b,d),(a,c,d),(b,c,d),其中能组成三角形的只有(b,c,d),所以以它们为边能作出三角形的概率是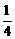 .
.
2. (2011山东滨州,23,9分)根据给出的下列两种情况,请用直尺和圆规找到一条直线,把△ABC恰好分割成两个等腰三角形(不写做法,但需保留作图痕迹);并根据每种情况分别猜想:∠A与∠B有怎样的数量关系时才能完成以上作图?并举例验证猜想所得结论。
(1)如图①△ABC中,∠C=90°,∠A=24°
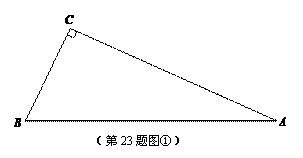
①作图:
②猜想:
③验证:
(2)如图②△ABC中,∠C=84°,∠A=24°.
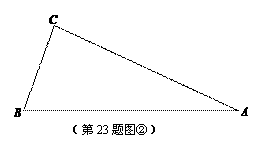

①作图:
②猜想:
③验证:
[答案]
(1)①作图:痕迹能体现作线段AB(或AC、或BC)的垂直平分线,或作∠ACD=∠A(或∠BCD=∠B)两类方法均可,
在边AB上找出所需要的点D,则直线CD即为所求………………2分
②猜想:∠A+∠B=90°,………………4分
③验证:如在△ABC中,∠A=30°,∠B=60°时,有∠A+∠B=90°,此时就能找到一条把△ABC恰好分割成两个等腰三角形的直线。………………5分
(2)答:①作图:痕迹能体现作线段AB(或AC、或BC)的垂直平分线,或作∠ACD=∠A或在线段CA上截取CD=CB三种方法均可。
在边AB上找出所需要的点D,则直线CD即为所求………………6分
②猜想:∠B=3∠A………………8分
③验证:如在△ABC中,∠A=32°,∠B=96,有∠B=3∠A,此时就能找到一条把△ABC恰好分割成两个等腰三角形的直线。………………9分
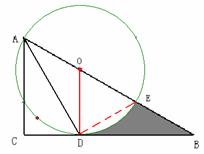
1. (2011江苏扬州,26,10分)已知,如图,在Rt△ABC中,∠C=90º,∠BAC的角平分线AD交BC边于D。
(1)以AB边上一点O为圆心,过A,D两点作⊙O(不写作法,保留作图痕迹),再判断直线BC与⊙O的位置关系,并说明理由;
(2)若(1)中的⊙O与AB边的另一个交点为E,AB=6,BD=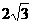 , 求线段BD、BE与劣弧DE所围成的图形面积。(结果保留根号和
, 求线段BD、BE与劣弧DE所围成的图形面积。(结果保留根号和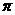 )
)
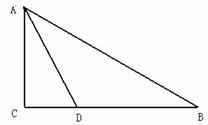
[答案](1)如图,作AD的垂直平分线交AB于点O,O为圆心,OA为半径作圆。
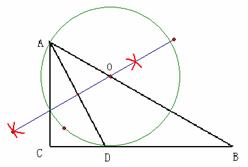
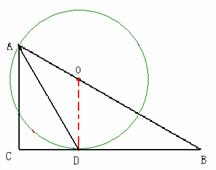
判断结果:BC是⊙O的切线。连结OD。
∵AD平分∠BAC ∴∠DAC=∠DAB
∵OA=OD ∴∠ODA=∠DAB
∴∠DAC=∠ODA ∴OD∥AC ∴∠ODB=∠C
∵∠C=90º ∴∠ODB=90º 即:OD⊥BC
∵OD是⊙O的半径 ∴ BC是⊙O的切线。
(2) 如图,连结DE。
设⊙O的半径为r,则OB=6-r,
在Rt△ODB中,∠ODB=90º,
∴ 0B2=OD2+BD2 即:(6-r)2=
r2+(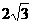 )2
)2
∴r=2 ∴OB=4 ∴∠OBD=30º,∠DOB=60º
∵△ODB的面积为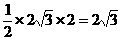 ,扇形ODE的面积为
,扇形ODE的面积为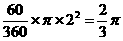
∴阴影部分的面积为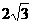 -
-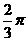 。
。
6.
1.
10.
9.
8.
7.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com