
题目列表(包括答案和解析)
2.执信中学2008-2009学年度高三数学试卷
知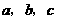 为
为 的三个内角
的三个内角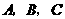 的对边,向量
的对边,向量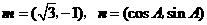 .若
.若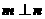 ,且
,且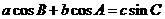 ,则角
,则角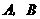 的大小分别为( )
的大小分别为( )
A.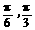 B.
B.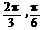 C.
C.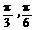 D.
D.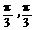
答案:C
解析:由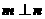 可得
可得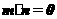 即
即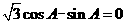 所以角
所以角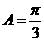 ,
,
且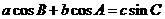 及
及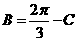 可得
可得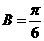
考点2 利用数量积处理夹角的范围
题型1:求夹角范围
[例5]已知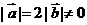 ,且关于
,且关于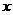 的方程
的方程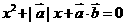 有实根,则
有实根,则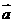 与
与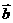 的夹角的取值范围是 ( )
的夹角的取值范围是 ( )
A.[0,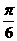 ] B.
] B.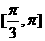 C.
C.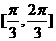 D.
D.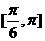
[解题思路]:要求两向量夹角θ的取值范围,可先求cosθ的取值范围.
解析:由关于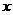 的方程
的方程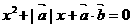 有实根,得:
有实根,得: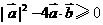
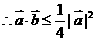 .设向量
.设向量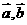 的夹角为θ,则cosθ=
的夹角为θ,则cosθ=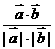 ,又
,又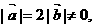
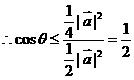 ,∴θ∈
,∴θ∈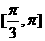 .[答案] B.
.[答案] B.
[名师指引]要求两向量夹角θ的取值范围,可先求cosθ的取值范围.
[新题导练]
1.(广东省普宁市城东中学2009届高三上学期第三次月考)
已知向量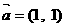 ,
,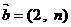 ,若
,若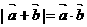 ,则
,则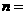 ( )
( )
A.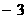 B.
B.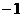 C.
C.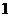 D.
D.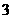
答案:D解析: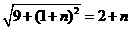 解得
解得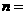
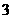
3.重难点:.
(1) 向量数量积与向量加、减、数乘运算的区别
问题1: 两个向量的数量积是一个实数,向量加、减、数乘运算的运算结果是向量。
例:规定, ·
·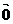 =
=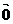 ·
· =0(不是零向量
=0(不是零向量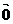 ,注意与λ
,注意与λ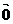 =
=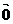 (λ∈R)区别)
(λ∈R)区别)
(2)向量数量积与实数相关概念的区别
问题2: 表示方法的区别
数量积的记号是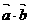 ,不能写成
,不能写成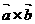 ,也不能写成
,也不能写成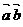 (所以有时把数量积称为“点乘”,记号
(所以有时把数量积称为“点乘”,记号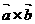 另外有定义,称为“叉乘”).
另外有定义,称为“叉乘”).
问题3:相关概念及运算的区别
⑴ 若a、b为实数,且 a·b=0,则有a=0或b=0,但 ·
· =0却不能得出
=0却不能得出 =
=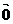 或
或 =
=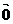 .因为只要
.因为只要 ⊥
⊥ 就有
就有 ·
· =0,而不必
=0,而不必 =
=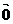 或
或 =
=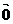 .
.
 ⑵ 若a、b、c∈R,且a≠0,则由ab=ac可得b=c,但由
⑵ 若a、b、c∈R,且a≠0,则由ab=ac可得b=c,但由 ·
· =
= ·
·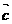 及
及 ≠0却不能推出
≠0却不能推出 =
=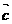 .因若
.因若 、
、 夹角为θ1,
夹角为θ1, 、
、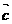 夹角为θ2,则由
夹角为θ2,则由 ·
· =
= ·
·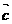 得|
得| |·|
|·| |cosθ1=|
|cosθ1=| |·|
|·|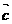 |cosθ2及|
|cosθ2及| |≠0,只能得到|
|≠0,只能得到| |cosθ1=|
|cosθ1=|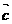 |cosθ2,即
|cosθ2,即 、
、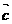 在
在 方向上投影相等,而不能得出
方向上投影相等,而不能得出 =
=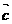 (见图).
(见图).
⑶ 若a、b、c∈R,则a(bc)=(ab)c(结合律)成立,但对于向量 、
、 、
、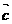 ,则(
,则( ·
· )·
)·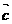 与
与 ·(
·( ·
·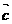 )都是无意义的,这是因为
)都是无意义的,这是因为 ·
· 与
与 ·
·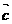 是数量,已不再是向量了,而数量与向量是没有点乘定义的.同时,(
是数量,已不再是向量了,而数量与向量是没有点乘定义的.同时,( ·
· )
)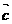 ≠
≠ (
( ·
·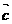 ),这是因为数量
),这是因为数量 ·
· 与向量
与向量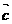 相乘是与
相乘是与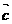 共线的向量,而数量
共线的向量,而数量 ·
·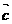 与向量
与向量 相乘则是与
相乘则是与 共线的向量,所以一般二者是不等的.这就是说,向量的数量积是不满足结合律的.
共线的向量,所以一般二者是不等的.这就是说,向量的数量积是不满足结合律的.
⑷ 若a、b∈R,则|a·b|=|a|·|b|,但对于向量 、
、 ,却有|
,却有| ·
· |≤|
|≤| |·|
|·| |,等号当且仅当
|,等号当且仅当 ∥
∥ 时成立.这是因为|
时成立.这是因为| ·
· |=|
|=| |·|
|·| |·|cosθ|而|cosθ|≤1.
|·|cosθ|而|cosθ|≤1.
★ 热 点 考 点 题 型 探 析★
考点一:平面向量数量积的运算
题型1. 求数量积、求模、求夹角
[例1] 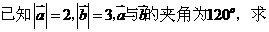
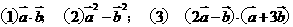 ;
;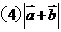
[解题思路]: 直接用定义或性质计算
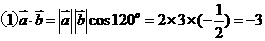 解析:
解析:
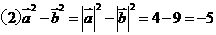
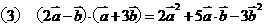
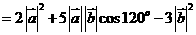
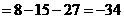
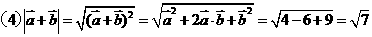
[例2]
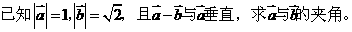
[解题思路]: 考虑公式cosq =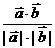 。
。
解析: 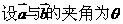
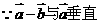
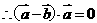
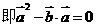
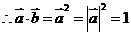
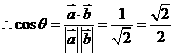
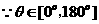
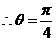
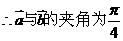
[名师指引]注意公式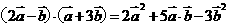 ,当知道
,当知道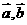 的模及它们的夹角可求
的模及它们的夹角可求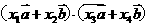 的数量积,反之知道
的数量积,反之知道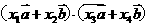 的数量积及
的数量积及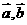 的模则可求它们的夹角。
的模则可求它们的夹角。
题型2。利用数量积解决垂直问题
[例3] 若非零向量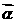 、
、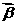 满足
满足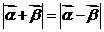 ,证明:
,证明: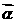
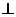
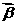
[解题思路]: 只须证明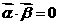 。
。
解析: [证明]由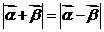 得:
得: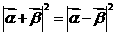
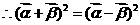
展开得: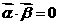 ,故
,故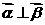
[例4] 在△ABC中,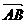 =(2, 3),
=(2, 3),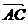 =(1, k),且△ABC的一个内角为直角,
=(1, k),且△ABC的一个内角为直角,
求k值
[解题思路]:注意分情况计论
解析:当A = 90°时,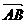 ×
×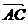 = 0,∴2×1 +3×k = 0 ∴k =
= 0,∴2×1 +3×k = 0 ∴k =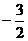
当B = 90°时,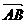 ×
×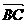 = 0,
= 0,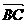 =
=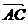 -
-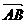 = (1-2,
k-3) = (-1, k-3)
= (1-2,
k-3) = (-1, k-3)
∴2×(-1) +3×(k-3) = 0 ∴k =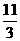
当C= 90°时,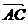 ×
×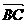 = 0,∴-1 + k(k-3) = 0 ∴k =
= 0,∴-1 + k(k-3) = 0 ∴k =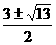
[名师指引]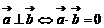 是一个常用的结论。
是一个常用的结论。
[新题导练]
2.难点:掌握两个向量共线、垂直的几何判断,会证明两向量垂直,以及能解决一些简单问题
1.重点:掌握平面向量数量积运算规律;能利用数量积的5个重要性质及数量积运算规律解决有关问题;
8.两向量夹角的余弦(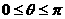 ) cosq =
) cosq = 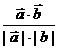
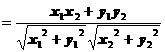
★ 重 难 点 突 破 ★
7.向量垂直的判定:设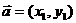 ,
,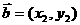 ,则
,则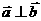

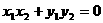
6.平面内两点间的距离公式
如果表示向量 的有向线段的起点和终点的坐标分别为
的有向线段的起点和终点的坐标分别为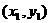 、
、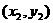 ,
,
那么: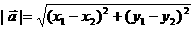
5.平面两向量数量积的坐标表示
已知两个非零向量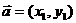 ,
,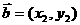 ,设
,设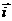 是
是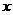 轴上的单位向量,
轴上的单位向量,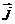 是
是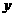 轴上的单位向量,那么
轴上的单位向量,那么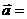
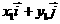 ,
, 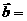
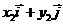 所以
所以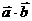
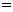
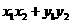
4. 平面向量数量积的运算律
交换律:  ×
×  =
=  ×
× 
数乘结合律: (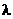
 )×
)× =
=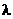 (
( ×
× ) =
) =  ×(
×(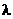
 )
)
分配律: ( +
+  )×
)×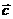 =
=  ×
×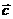 +
+  ×
×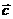
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com