
题目列表(包括答案和解析)
4.已知结论:“在正三角形ABC中,若D是边BC的中点,G是三角形ABC的重心,则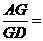
2“。若把该结论推广到空间,则有结论:“在棱长都相等的四面体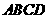 中,若
中,若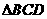 的中心为
的中心为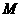 ,四面体内部一点
,四面体内部一点 到四面体各面的距离都相等,则
到四面体各面的距离都相等,则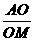 =
=
A.1 B.2 C.3 D.4
3.下列命题错误的是
A.命题“若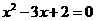 ,则
,则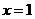 “的逆否命题为”若
“的逆否命题为”若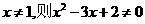 “
“
B.若命题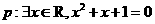 ,则
,则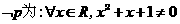
C.若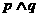 为假命题,则
为假命题,则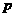 ,
,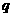 均为假命题
均为假命题
D.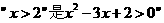 的充分不必要条件
的充分不必要条件
2.若复数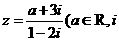 是虚数单位),且
是虚数单位),且 是纯虚数,则
是纯虚数,则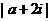 等于
等于
A.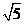 B.
B.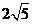 C.
C.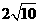 D.40
D.40
1.设全集为,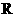 ,集合
,集合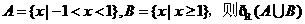 等于
等于
A.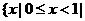 B.
B.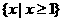 C.
C.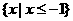 D.
D.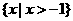
22. (本小题满分14分)已知椭圆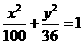 的左右顶点分别为A1,A2,是椭圆上不同于的动点,直线P A1、PA2与右准线分别交于M、N。
的左右顶点分别为A1,A2,是椭圆上不同于的动点,直线P A1、PA2与右准线分别交于M、N。
(1)求证: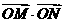 为定值;
为定值;
(2)求证:以MN为直径的圆与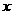 轴交于两个不同的定点,并求这两点的坐标;
轴交于两个不同的定点,并求这两点的坐标;
(3)当以MN为直径的圆的面积最小时,在焦三角形PF1F2中,求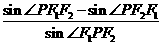 的值。
的值。
2009届江西省中点中学联考盟校第一次模拟考试
21. (本小题满分12分)已知函数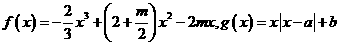
(1)判断函数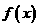 在R上的单调性,并证明你的结论;
在R上的单调性,并证明你的结论;
(2)设常数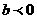 且
且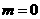 ,若对任意的实数
,若对任意的实数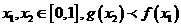 恒成立,求出实数
恒成立,求出实数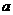 的取值范围。
的取值范围。
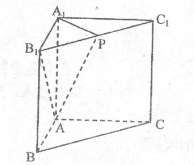
19. (本小题满分12分)在三棱柱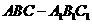 中,侧面
中,侧面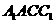 是矩形,
是矩形,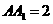 ,
,
 平面
平面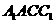
 平面
平面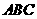 ,
,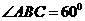 ,P是
,P是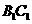 的中点,
的中点,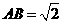
(1)求证: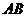
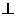
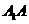
(2)求二面角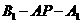 的正切值。
的正切值。
20(本小题满分12分)已知二函数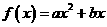 (其中
(其中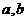 是常数),数列
是常数),数列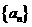 的前
的前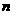 项和为
项和为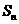 ,且
,且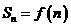 ,又数列
,又数列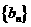 是等比数列,且
是等比数列,且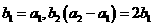
(1)
求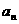 与
与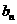
(2)
若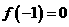 ,且
,且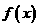 的最小值为
的最小值为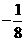 ,数列
,数列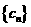 满足
满足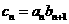 ,求
,求
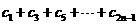 的值
的值
18. (本小题满分12分)现有甲、乙两个盒子,甲盒子里盛有4个白球和4个红球,乙盒子里盛有3个白球和若干个红球,若从乙盒子里任取两个球取得同色球的概率为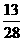 。
。
(1)求乙盒子中红球的个数;
(2)从甲、乙盒子里任取两个球进行交换,若交换后乙盒子里的白球数和红球数相等,就说这次交换是成功的,试求进行一次这样的交换成功的概率是多少?
17.(本小题满分12分)在锐角三角形ABC中,角A、B、C多对边分别为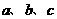 ,且
,且
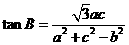
(1) 求B
(2)
求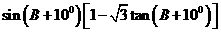 的值
的值
16.设函数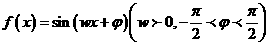 ,给出一下四个结论:①它的周期为; ②它的图像关于直线
,给出一下四个结论:①它的周期为; ②它的图像关于直线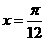 对称;③它的图像关于点
对称;③它的图像关于点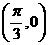 对称;④在区间
对称;④在区间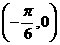 上是增函数,以其中连个论断为条件,另两个论断做结论写出你认为正确的一个命题(用序号表示)
上是增函数,以其中连个论断为条件,另两个论断做结论写出你认为正确的一个命题(用序号表示)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com