
题目列表(包括答案和解析)
3、 有穷数列与无穷数列;
2、 数列的项与项数;
1、 数列的定义及表示方法;
本章是高考命题的主体内容之一,应切实进行全面、深入地复习,并在此基础上,突出解决下述几个问题:
(1)等差、等比数列的证明须用定义证明,值得注意的是,若给出一个数列的前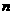 项和
项和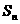 ,则其通项为
,则其通项为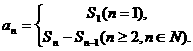 若
若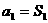 满足
满足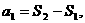 则通项公式可写成
则通项公式可写成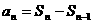 。
。
(2)数列计算是本章的中心内容,利用等差数列和等比数列的通项公式、前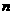 项和公式及其性质熟练地进行计算,是高考命题重点考查的内容。
项和公式及其性质熟练地进行计算,是高考命题重点考查的内容。
(3)解答有关数列问题时,经常要运用各种数学思想.善于使用各种数学思想解答数列题,是我们复习应达到的目标。
①函数思想:等差等比数列的通项公式求和公式都可以看作是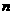 的函数,所以等差等比数列的某些问题可以化为函数问题求解。
的函数,所以等差等比数列的某些问题可以化为函数问题求解。
②分类讨论思想:用等比数列求和公式应分为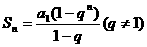 及
及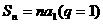 ;已知
;已知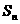 求
求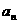 时,也要进行分类;
时,也要进行分类;
③整体思想:在解数列问题时,应注意摆脱呆板使用公式求解的思维定势,运用整体思想求解。
(4)在解答有关的数列应用题时,要认真地进行分析,将实际问题抽象化,转化为数学问题,再利用有关数列知识和方法来解决。解答此类应用题是数学能力的综合运用,决不是简单地模仿和套用所能完成的,特别注意与年份有关的等比数列的第几项不要弄错。
3.导数与解析几何或函数图象的混合问题是一种重要类型,也是高考中考察综合能力的一个方向,应引起注意。
(1)刻画函数(比初等方法精确细微);
(2)同几何中切线联系(导数方法可用于研究平面曲线的切线);
(3)应用问题(初等方法往往技巧性要求较高,而导数方法显得简便)等关于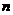 次多项式的导数问题属于较难类型。
次多项式的导数问题属于较难类型。
2.关于函数特征,最值问题较多,所以有必要专项讨论,导数法求最值要比初等方法快捷简便。
(四)单调区间的求解过程,已知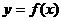
(1)分析
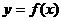 的定义域;(2)求导数
的定义域;(2)求导数
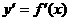 ;(3)解不等式
;(3)解不等式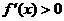 ,解集在定义域内的部分为增区间;(4)解不等式
,解集在定义域内的部分为增区间;(4)解不等式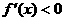 ,解集在定义域内的部分为减区间。
,解集在定义域内的部分为减区间。
我们在应用导数判断函数的单调性时一定要搞清以下三个关系,才能准确无误地判断函数的单调性。以下以增函数为例作简单的分析,前提条件都是函数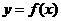 在某个区间内可导。
在某个区间内可导。
③求极值、求最值。
注意:极值≠最值。函数f(x)在区间[a,b]上的最大值为极大值和f(a) 、f(b)中最大的一个。最小值为极小值和f(a) 、f(b)中最小的一个。
f/(x0)=0不能得到当x=x0时,函数有极值。
但是,当x=x0时,函数有极值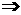 f/(x0)=0
f/(x0)=0
判断极值,还需结合函数的单调性说明。
(三)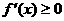 与
与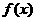 为增函数的关系。
为增函数的关系。
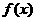 为增函数,一定可以推出
为增函数,一定可以推出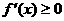 ,但反之不一定,因为
,但反之不一定,因为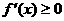 ,即为
,即为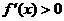 或
或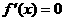 。当函数在某个区间内恒有
。当函数在某个区间内恒有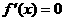 ,则
,则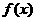 为常数,函数不具有单调性。∴
为常数,函数不具有单调性。∴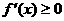 是
是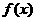 为增函数的必要不充分条件。
为增函数的必要不充分条件。
函数的单调性是函数一条重要性质,也是高中阶段研究的重点,我们一定要把握好以上三个关系,用导数判断好函数的单调性。因此新教材为解决单调区间的端点问题,都一律用开区间作为单调区间,避免讨论以上问题,也简化了问题。但在实际应用中还会遇到端点的讨论问题,要谨慎处理。
(二)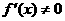 时,
时,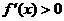 与
与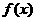 为增函数的关系。
为增函数的关系。
若将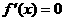 的根作为分界点,因为规定
的根作为分界点,因为规定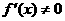 ,即抠去了分界点,此时
,即抠去了分界点,此时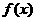 为增函数,就一定有
为增函数,就一定有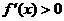 。∴当
。∴当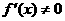 时,
时,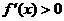 是
是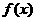 为增函数的充分必要条件。
为增函数的充分必要条件。
(一)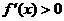 与
与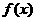 为增函数的关系。
为增函数的关系。
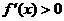 能推出
能推出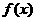 为增函数,但反之不一定。如函数
为增函数,但反之不一定。如函数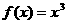 在
在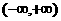 上单调递增,但
上单调递增,但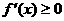 ,∴
,∴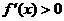 是
是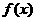 为增函数的充分不必要条件。
为增函数的充分不必要条件。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com