
题目列表(包括答案和解析)
已知正项数列 的前n项和
的前n项和 满足:
满足: ,
,
(1)求数列 的通项
的通项 和前n项和
和前n项和 ;
;
(2)求数列 的前n项和
的前n项和 ;
;
(3)证明:不等式  对任意的
对任意的 ,
, 都成立.
都成立.
【解析】第一问中,由于 所以
所以
两式作差 ,然后得到
,然后得到
从而 得到结论
得到结论
第二问中, 利用裂项求和的思想得到结论。
利用裂项求和的思想得到结论。
第三问中,

又
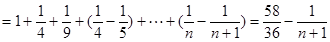
结合放缩法得到。
解:(1)∵ ∴
∴
∴
∴ ∴
∴  ………2分
………2分
又∵正项数列 ,∴
,∴ ∴
∴
又n=1时,
∴ ∴数列
∴数列 是以1为首项,2为公差的等差数列……………3分
是以1为首项,2为公差的等差数列……………3分
∴ …………………4分
…………………4分
∴ …………………5分
…………………5分
(2) …………………6分
…………………6分
∴
 …………………9分
…………………9分
(3)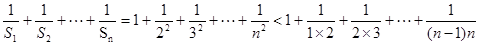
 …………………12分
…………………12分
又

 ,
,
∴不等式  对任意的
对任意的 ,
, 都成立.
都成立.
已知幂函数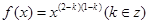 满足
满足 。
。
(1)求实数k的值,并写出相应的函数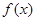 的解析式;
的解析式;
(2)对于(1)中的函数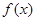 ,试判断是否存在正数m,使函数
,试判断是否存在正数m,使函数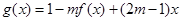 ,在区间上的最大值为5。若存在,求出m的值;若不存在,请说明理由。
,在区间上的最大值为5。若存在,求出m的值;若不存在,请说明理由。
【解析】本试题主要考查了函数的解析式的求解和函数的最值的运用。第一问中利用,幂函数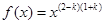 满足
满足 ,得到
,得到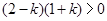
因为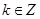 ,所以k=0,或k=1,故解析式为
,所以k=0,或k=1,故解析式为
(2)由(1)知,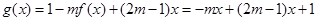 ,
, ,因此抛物线开口向下,对称轴方程为:
,因此抛物线开口向下,对称轴方程为: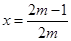 ,结合二次函数的对称轴,和开口求解最大值为5.,得到
,结合二次函数的对称轴,和开口求解最大值为5.,得到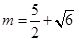
(1)对于幂函数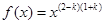 满足
满足 ,
,
因此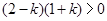 ,解得
,解得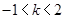 ,………………3分
,………………3分
因为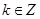 ,所以k=0,或k=1,当k=0时,
,所以k=0,或k=1,当k=0时, ,
,
当k=1时, ,综上所述,k的值为0或1,
,综上所述,k的值为0或1, 。………………6分
。………………6分
(2)函数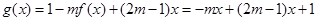 ,………………7分
,………………7分
由此要求 ,因此抛物线开口向下,对称轴方程为:
,因此抛物线开口向下,对称轴方程为: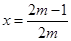 ,
,
当 时,
时,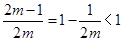 ,因为在区间
,因为在区间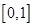 上的最大值为5,
上的最大值为5,
所以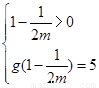 ,或
,或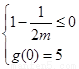 …………………………………………10分
…………………………………………10分
解得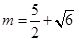 满足题意
满足题意
已知中心在坐标原点,焦点在 轴上的椭圆C;其长轴长等于4,离心率为
轴上的椭圆C;其长轴长等于4,离心率为 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点 (0,1), 问是否存在直线
(0,1), 问是否存在直线 与椭圆
与椭圆 交于
交于 两点,且
两点,且 ?若存在,求出
?若存在,求出 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
【解析】本试题主要考查了椭圆的方程的求解,直线与椭圆的位置关系的运用。
第一问中,可设椭圆的标准方程为
则由长轴长等于4,即2a=4,所以a=2.又 ,所以
,所以 ,
,
又由于
所求椭圆C的标准方程为
第二问中,
假设存在这样的直线 ,设
,设 ,MN的中点为
,MN的中点为
因为|ME|=|NE|所以MN EF所以
EF所以
(i)其中若 时,则K=0,显然直线
时,则K=0,显然直线 符合题意;
符合题意;
(ii)下面仅考虑 情形:
情形:
由 ,得,
,得,
 ,得
,得
代入1,2式中得到范围。
(Ⅰ) 可设椭圆的标准方程为
则由长轴长等于4,即2a=4,所以a=2.又 ,所以
,所以 ,
,
又由于
所求椭圆C的标准方程为
(Ⅱ) 假设存在这样的直线 ,设
,设 ,MN的中点为
,MN的中点为
因为|ME|=|NE|所以MN EF所以
EF所以
(i)其中若 时,则K=0,显然直线
时,则K=0,显然直线 符合题意;
符合题意;
(ii)下面仅考虑 情形:
情形:
由 ,得,
,得,
 ,得
,得 ……② ……………………9分
……② ……………………9分
则 .
.
代入①式得,解得 ………………………………………12分
………………………………………12分
代入②式得 ,得
,得 .
.
综上(i)(ii)可知,存在这样的直线 ,其斜率k的取值范围是
,其斜率k的取值范围是

为了解某班学生喜爱打羽毛球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
|
|
喜爱打羽毛球 |
不喜爱打羽毛球 |
合计 |
|
男生 |
|
5 |
|
|
女生 |
10 |
|
|
|
|
|
|
50 |
已知在全部50人中随机抽取1人抽到不喜爱打羽毛球的学生的概率
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打羽毛球与性别有关?说明你的理由;
(3)已知喜爱打羽毛球的10位女生中, 还喜欢打篮球,
还喜欢打篮球, 还喜欢打乒乓球,
还喜欢打乒乓球, 还喜欢踢足球,现在从喜欢打篮球、喜欢打乒乓球、喜欢踢足球的6位女生中各选出1名进行其他方面的调查,求女生
还喜欢踢足球,现在从喜欢打篮球、喜欢打乒乓球、喜欢踢足球的6位女生中各选出1名进行其他方面的调查,求女生 和
和 不全被选中的概率.下面的临界值表供参考:
不全被选中的概率.下面的临界值表供参考:
|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: 其中
其中 .)
.)
【解析】第一问利用数据写出列联表
第二问利用公式 计算的得到结论。
计算的得到结论。
第三问中,从6位女生中选出喜欢打篮球、喜欢打乒乓球、喜欢踢足球的各1名,其一切可能的结果组成的基本事件如下:
 ,
,
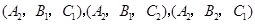 ,
,
基本事件的总数为8
用 表示“
表示“ 不全被选中”这一事件,则其对立事件
不全被选中”这一事件,则其对立事件 表示“
表示“ 全被选中”这一事件,由于
全被选中”这一事件,由于 由
由 2个基本事件由对立事件的概率公式得
2个基本事件由对立事件的概率公式得
解:(1) 列联表补充如下:
|
|
喜爱打羽毛球 |
不喜爱打羽毛球 |
合计 |
|
男生 |
20 |
5 |
25 |
|
女生 |
10 |
15 |
25 |
|
合计 |
30 |
20 |
50 |
(2)∵
∴有99.5%的把握认为喜爱打篮球与性别有关
(3)从6位女生中选出喜欢打篮球、喜欢打乒乓球、喜欢踢足球的各1名,其一切可能的结果组成的基本事件如下:
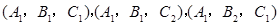 ,
,
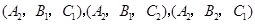 ,
,
基本事件的总数为8,
用 表示“
表示“ 不全被选中”这一事件,则其对立事件
不全被选中”这一事件,则其对立事件 表示“
表示“ 全被选中”这一事件,由于
全被选中”这一事件,由于 由
由 2个基本事件由对立事件的概率公式得
2个基本事件由对立事件的概率公式得 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com