练习册

  • 练习册
  • 试题
    当得.G点的坐标为. 【查看更多】

     

    题目列表(包括答案和解析)

    已知过点的动直线与抛物线相交于两点．当直线的斜率是时，．

    （１）求抛物线的方程；

    （２）设线段的中垂线在轴上的截距为，求的取值范围．

    【解析】（1）B,C，当直线的斜率是时，

    的方程为，即                                （1’）

    联立  得，         （3’）

    由已知  ,                    （4’）

    由韦达定理可得G方程为            （5’）

    （2）设：，BC中点坐标为               （6’）

    得 由得       （8’）

        

    BC中垂线为             （10’）

                      （11’）

     

    查看答案和解析>>

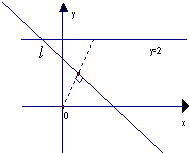    如图，在直角坐标系xoy中，坐标原点O（0，0），以动直线l：y=mx+n（m，n∈R）为轴翻折，使得每次翻折后点O都落在直线y=2上．
    （1）求以（m，n）为坐标的点的轨迹G的方程；
    （2）过点E（0，
    54
    ）作斜率为k的直线交轨迹G于M，N两点；（ⅰ）当+MN|=3时，求M，N两点的纵坐标之和；（ⅱ）问是否存在直线，使△OMN的面积等于某一给定的正常数，说明你的理由．

    查看答案和解析>>

    定义向量=（a，b）的“相伴函数”为f（x）=asinx+bcosx，函数f（x）=asinx+bcosx的“相伴向量”为=（a，b）（其中O为坐标原点），记平面内所有向量的“相伴函数”构成的集合为S。
    （1）设g（x）=3sin（x+）+4sinx，求证：g（x）∈S；
    （2）已知h（x）=cos（x+α）+2cosx，且h（x）∈S，求其“相伴向量”的模；
    （3）已知M（a，b）（b≠0）为圆C：（x-2）2+y2=1上一点，向量的“相伴函数”f（x）在x=x0处取得最大值，当点M在圆C上运动时，求tan2x0的取值范围。

    查看答案和解析>>

    已知双曲线C的中心为坐标原点O，右顶点为A(1，0)，G为双曲线C的右准线与x轴的交点，P、Q为双曲线C上不同两点，且满足≠0，=0．

    (Ⅰ)求双曲线C的方程；

    (Ⅱ)若直线FQ按向量a=(0，1)平移后所得直线与双曲线C交于不同两点M、N，当-≤≤-时，求直线PQ的斜率的取值范围．

    查看答案和解析>>

    定义向量=（a，b）的“相伴函数”为f（x）=asinx+bcosx，函数f（x）=asinx+bcosx的“相伴向量”为=（a，b）（其中O为坐标原点）．记平面内所有向量的“相伴函数”构成的集合为S．
    （1）设g（x）=3sin（x+）+4sinx，求证：g（x）∈S；
    （2）已知h（x）=cos（x+α）+2cosx，且h（x）∈S，求其“相伴向量”的模；
    （3）已知M（a，b）（b≠0）为圆C：（x-2）2+y2=1上一点，向量的“相伴函数”f（x）在x=x处取得最大值．当点M在圆C上运动时，求tan2x的取值范围．

    查看答案和解析>>


    同步练习册答案