
题目列表(包括答案和解析)
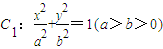 的左右焦点分别为F1,F2,O为坐标原点,过F2的直线l1与C1交于A,B两点,且△ABF1的周长为
的左右焦点分别为F1,F2,O为坐标原点,过F2的直线l1与C1交于A,B两点,且△ABF1的周长为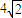 ,l1的倾斜角为α.
,l1的倾斜角为α.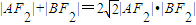
 .
.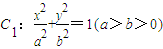 的左右焦点分别为F1,F2,O为坐标原点,过F2的直线l1与C1交于A,B两点,且△ABF1的周长为
的左右焦点分别为F1,F2,O为坐标原点,过F2的直线l1与C1交于A,B两点,且△ABF1的周长为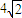 ,l1的倾斜角为α.
,l1的倾斜角为α.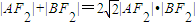
 .
.| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
| 2 |
(本题满分14分)
已知函数![]() 与函数
与函数![]() 的图像关于直线
的图像关于直线![]() 对称.
对称.
(1)试用含![]() 的代数式表示函数
的代数式表示函数![]() 的解析式,并指出它的定义域;
的解析式,并指出它的定义域;
(2)数列![]() 中,
中,![]() ,当
,当![]() 时,
时,![]() .数列
.数列![]() 中,
中,![]() ,
,![]() .点
.点![]() 在函数
在函数![]() 的图像上,求
的图像上,求![]() 的值;
的值;
(3)在(2)的条件下,过点![]() 作倾斜角为
作倾斜角为![]() 的直线
的直线![]() ,则
,则![]() 在y轴上的截距为
在y轴上的截距为![]()
![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
(1)试用含a的代数式表示函数f(x)的解析式,并指出它的定义域;
(2)数列{an}中,a1=1,当n≥2时,an>a1.数列{bn}中,b1=2,Sn=b1+b2+…+bn.点Pn(an,![]() ) (n=1,2, 3,…)在函数f(x)的图象上,求a的值;
) (n=1,2, 3,…)在函数f(x)的图象上,求a的值;
(3)在(2)的条件下,过点Pn作倾斜角为![]() 的直线ln,则ln在y轴上的截距为
的直线ln,则ln在y轴上的截距为![]() (bn+1)(n=1,2, 3,…),求数列{an}的通项公式.
(bn+1)(n=1,2, 3,…),求数列{an}的通项公式.
一、选择题:
1.C 2.D 3.C 4.A 5.B 6.C 7.B 8.A 9.D 10.A 11.A 12.C
二、填空题:
13..files/image250.gif) 14. 26 15. -3 16.
14. 26 15. -3 16. .files/image252.gif) 17. 3
18.
17. 3
18. .files/image254.gif)
19..files/image256.gif) 20.(0,1) 21.
20.(0,1) 21. .files/image258.gif) 22.
22..files/image260.gif) 23.765 24.5
23.765 24.5
25.2
26..files/image262.gif)
三、解答题:
27、解:(1)∵cos3x=4cos3x-3cosx,则.files/image193.gif) =4cos2x-3=2cos2x-1
=4cos2x-3=2cos2x-1
∴f(x)=2cos2x-1+2sin2x
=2.files/image265.gif) sin(2x+
sin(2x+.files/image242.gif) )-1
)-1
在2x+.files/image242.gif) =2kπ+
=2kπ+.files/image269.gif) 时,f(x)取得最大值2
时,f(x)取得最大值2.files/image265.gif) -1
-1
即在x=kπ+.files/image271.gif) (k∈Z)时,f(x)取得最大值2
(k∈Z)时,f(x)取得最大值2.files/image265.gif) -1
-1
(2)∵f(x)=2.files/image265.gif) sin(2x+
sin(2x+.files/image242.gif) )-1
)-1
要使f(x)递减,x满足2kπ+.files/image269.gif) ≤2x+
≤2x+.files/image242.gif) ≤2kπ+
≤2kπ+.files/image274.gif)
即kπ+.files/image271.gif) ≤x≤kπ+
≤x≤kπ+.files/image277.gif) (k∈Z)
(k∈Z)
又∵cosx≠0,即x≠kπ+.files/image269.gif) (k∈Z)
(k∈Z)
|