
题目列表(包括答案和解析)
(本题满分12分)设函数f(x)=x3- ax2+3x+5(a>0).
ax2+3x+5(a>0).
(1)已知f(x)在R上是单调函数,求a的取值范围;
(2)若a=2,且当x∈[1,2]时,f(x)≤m恒成立,求实数m的取值范围.
(本题满分12分)设函数f(x)=x3- ax2+3x+5(a>0).
ax2+3x+5(a>0).
(1)已知f(x)在R上是单调函数,求a的取值范围;
(2)若a=2,且当x∈[1,2]时,f(x)≤m恒成立,求实数m的取值范围.
 ax2+3x+5(a>0).
ax2+3x+5(a>0).(本小题满分12分)已知函数f(x)=x3-ax2-3x.
(1)若f(x)在x∈[1,+∞)上是增函数,求实数a的取值范围;
(2)若x=3是f(x)的极值点,求f(x)在x∈[1,a]上的最小值和最大值.
(本小题满分12分)已知函数f(x)=x3+ax2+bx+c在x=-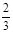 与x=1时都取得极值.
与x=1时都取得极值.
(1)求a、b的值与函数f(x)的单调区间;
(2)xÎ〔-1,2〕,不等式f(x)<c2恒成立,求c的取值范围.
1-5.ADDCA 6-10:BBC

 9.如图设点P为AB的三等分点,要使△PBC的面积不小于
9.如图设点P为AB的三等分点,要使△PBC的面积不小于 ,则点P只能在
,则点P只能在
AP上选取,由几何概型的概率
公式得所求概率为 .故选A.
.故选A.
10.如图:易得答案选D.
11.由率分布直方图知,及格率= =80%,
=80%,
及格人数=80%×1000=800,优秀率= %.
%.
12.
13.
14.在平面直角坐标系中,曲线 和
和 分别表示圆
分别表示圆 和直线
和直线 ,易知
,易知 =
=
15. C为圆周上一点,AB是直径,所以AC⊥BC,而BC=3,AB=6,得∠BAC=30°,进而得∠B=60°,所以∠DCA=60°,又∠ADC=90°,得∠DAC=30°,

三、解答题
16.解:(1) ………2分
………2分
 ………3分
………3分
 ………5分
………5分
所以函数 的最小正周期
的最小正周期 ………6分
………6分
(2)当 ,
,

 ,
,
∴当 时,
时, 有最大值
有最大值 ;
………10分
;
………10分
当 ,即
,即 时,
时, 有最小值
有最小值 . ………12分
. ………12分
17. 解:(I)由函数 是奇函数,∴
是奇函数,∴ ,
, .
2分
.
2分
(II)由
 x3+4cx,
x3+4cx,
有 ax2+
ax2+ .
.
∴ 解得
解得  6分
6分
故 .
………………………………………………8分
.
………………………………………………8分
?Ⅲ? f(x)=
f(x)= x3-8x,∴
x3-8x,∴ 2x2-8=2(x+2)(x-2).
10分
2x2-8=2(x+2)(x-2).
10分
令 >0得x<-2或x>2 , 令
>0得x<-2或x>2 , 令 <0得-2<x<2.
12分
<0得-2<x<2.
12分
∴函数 的单调增区间为(
的单调增区间为( ,[2,+
,[2,+
 ;单调减区间为[-2,2]. 14分
;单调减区间为[-2,2]. 14分
(或增区间为 ,(2,+
,(2,+
 ;减区间为(-2,2))
;减区间为(-2,2))
18. 证明:(1)取PD中点Q, 连EQ , AQ
, 则 ……………………………………1分
……………………………………1分

 …………………………………………2分
…………………………………………2分
 ………………3分
………………3分
 ………………………5分
………………………5分
 (2)
(2) 
 . ………………………………………10分
. ………………………………………10分
解:(3) …………………………………11分
…………………………………11分
 . ………………………………14分
. ………………………………14分
19. 解:满足条件的 点共有
点共有 个
……………………1分
个
……………………1分
(1)正好在第二象限的点有
 ,
, ,
, ,
, ,
, ,
, ………………3分
………………3分
故点 正好在第二象限的概率P1=
正好在第二象限的概率P1= .
………………4分
.
………………4分
(2)在x轴上的点有 ,
, ,
, ,
, ,
, ,
, ……6分
……6分
故点 不在x轴上的概率P2=1-
不在x轴上的概率P2=1- =
= .
……………………8分
.
……………………8分
(3)在所给区域内的点有 ,
, ,
, ,
, ,
, ,
, ………10分
………10分
故点 在所给区域上的概率
在所给区域上的概率 ……………………11分
……………………11分
答:(1)点 正好在第二象限的概率是
正好在第二象限的概率是 ,(2)点
,(2)点 不在x轴上的概率是
不在x轴上的概率是 ,(3)点
,(3)点 在所给区域上的概率
在所给区域上的概率 …………………14分
…………………14分
20. 解:(1)令 ………2分
………2分
由
(II)
设 ………………………………………………9分
………………………………………………9分
两边同乘以
故数列 等差数列 ……………………………………………12分
等差数列 ……………………………………………12分
A(0,b)知
 设
设 ,
,
得 …2分
…2分
因为点P在椭圆上,所以 …………4分
…………4分
整理得2b2= ,故椭圆的离心率e=
,故椭圆的离心率e= ………6分
………6分
⑵由⑴知 ,
,  于是F(-
于是F(- a,0) Q
a,0) Q ,
,
△AQF的外接圆圆心为( a,0),半径r=
a,0),半径r= |FQ|=a……………………11分
|FQ|=a……………………11分
所以 ,解得a=2,∴c=1,b=
,解得a=2,∴c=1,b= ,所求椭圆方程为
,所求椭圆方程为 ……14分
……14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com