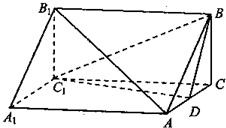如图，三棱柱ABC-A₁B₁C₁中，AA₁⊥面ABC，BC⊥AC，BC=AC=2，D为AC的中点．
（1）求证：AB₁∥面BDC₁；
（2）若AA₁=3，求二面角C₁-BD-C的余弦值．

查看答案和解析>>

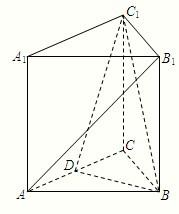如图，三棱柱ABC-A₁B₁C₁，A₁A⊥底面ABC，且△ABC为正三角形，A₁A=AB=6，D为AC中点．
（Ⅰ）求三棱锥C₁-BCD的体积；
（Ⅱ）求证：平面BC₁D⊥平面ACC₁A₁；
（Ⅲ）求证：直线AB₁∥平面BC₁D．

查看答案和解析>>

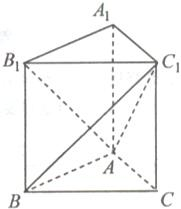如图，三棱柱A₁B₁C₁-ABC中，平面A₁AB⊥平面ABC，平面A₁AC⊥平面ABC，∠BAC=90°，AB=AC=2，AA₁=3．
（Ⅰ） 求证：AA₁⊥平面ABC；
（Ⅱ） 求异面直线AB₁与BC₁所成的角的余弦值；
（Ⅲ） 求点B₁到平面ABC₁的距离．

查看答案和解析>>

（2013•天津）如图，三棱柱ABC-A₁B₁C₁中，侧棱A₁A⊥底面ABC，且各棱长均相等．D，E，F分别为棱AB，BC，A₁C₁的中点．
（Ⅰ）证明：EF∥平面A₁CD；
（Ⅱ）证明：平面A₁CD⊥平面A₁ABB₁；
（Ⅲ）求直线BC与平面A₁CD所成角的正弦值．

查看答案和解析>>

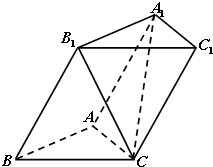如图，三棱柱ABC-A₁B₁C₁的各棱长均为2，侧面BCC₁B₁⊥底面ABC，侧棱BB₁与底面ABC所成的角为60°．
（Ⅰ）求直线A₁C与底面ABC所成的角；
（Ⅱ）在线段A₁C₁上是否存在点P，使得平面B₁CP⊥平面ACC₁A₁？若存在，求出C₁P的长；若不存在，请说明理由．

查看答案和解析>>

1．B　2．（文）B　（理）D　3．C　4．B　5．C　6．A　7．（文）A　（理）D　8．D　9．B　10．D　11．A　12．B

13．2　　14．（0，）　　15．　　16．

17．恰有3个红球的概率

　　有4个红球的概率

　　至少有3个红球的概率

18．∵　

　　（1）最小正周期　

　　（2），

　　∴　时　，∴　，　　∴　a＝1．

19．（甲）（1）以DA、DC、DP所在直线分别为x轴、y轴、z轴建立空间坐标系（2，0，0），B（2，2，0），C（0，2，0）设P（0，0，2m）（1，1，m），∴　（-1，1，m），＝（0，0，2m）

　　∴　，，

　　∴　点E坐标是（1，1，1）

　　（2）∵　平面PAD，　∴　可设F（x，0，z）＝（x-1，-1，z-1）

　　∵　EF⊥平面PCB　∴　，-1，2，0，

　　∵　　∴　，-1，0，2，-2

　　∴　点F的坐标是（1，0，0），即点F是AD的中点．

　　（乙）（1）证明：∵　是菱形，∠＝60°△是正三角形

　　又∵　

　　（2）　∴　∠BEM为所求二面角的平面角

　　△中，60°，Rt△中，60°

　　∴　，　∴　所求二面角的正切值是2；

　　（3）．

20．（1）设f（x）图像上任一点坐标为（x，y），点（x，y）关于点A（0，1）的对称点（-x，2-y）在h（x）图像上

　　∴　，　∴　，即　

　　（2）（文）：，即在（0，上递减，　∴　a≤-4

　　（理）：，　∵　　在（0，上递减，

　　∴　在（0，时恒成立．即　在（0，时恒成立．

∵　（0，时，　∴．

21．（1）2007年A型车价为32＋32×25％＝40（万元）

　　设B型车每年下降d万元，2002，2003……2007年B型车价格为：（公差为-d）

　　，……　∴　≤40×90％　∴　46-5d≤36　d≥2

　　故每年至少下降2万元

　　（2）2007年到期时共有钱

　　＞33（1＋0.09＋0.00324＋……）＝36.07692＞36（万元）

　　故5年到期后这笔钱够买一辆降价后的B型车

22．（1）如图，以AB所在直线为x轴，AB中垂线为y轴建立直角坐标系，A（-1，0），B（1，0）

　　设椭圆方程为：

令　∴

　　∴　椭圆C的方程是：

　　（2）（文）l⊥AB时不符合，

　　∴　设l：

　　设M（，），N（，），

　　∵　　　∴　，即，

　　∴　l：，即　经验证：l与椭圆相交，

　　∴　存在，l与AB的夹角是．

　　（理），，l⊥AB时不符，设l：y＝kx＋m（k≠0）

　　由　

　　M、N存在

　　设M（，），N（，），MN的中点F（，）

　　∴　，

　　∴　　　∴　

　　∴　　　∴　且

　　∴　l与AB的夹角的范围是，．