
题目列表(包括答案和解析)
 A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线ρsin(θ+
A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线ρsin(θ+| π | 3 |
 A.(不等式选做题)若关于x的不等式|x+3|-|x+2|≥log2a有解,则实数a的取值范围是:
A.(不等式选做题)若关于x的不等式|x+3|-|x+2|≥log2a有解,则实数a的取值范围是:| PB |
| PA |
| 1 |
| 2 |
| PC |
| PD |
| 1 |
| 3 |
| BC |
| AD |
|
| 2 |
| cosθ-sinθ |
| 2 |
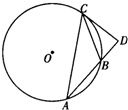 A.(不等式选做题)
A.(不等式选做题)| 3 |
| π |
| 3 |
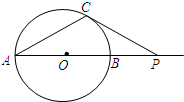 A.不等式
A.不等式| x-2 |
| x2+3x+2 |
| 3 |
|
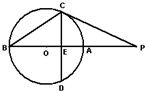 A.(不等式选做题)不等式|3x-6|-|x-4|>2x的解集为
A.(不等式选做题)不等式|3x-6|-|x-4|>2x的解集为| π |
| 4 |
| 2 |
一、选择题:
1.A 2.A 3.D 4.C
5.B 6.D 7.D 8.B
9.C 10.C 11.D 12.C
二、填空题:
13.-252
14. .files/image148.gif) 15. -3 16.
15. -3 16. .files/image150.gif) 17.
17..files/image152.gif)
三、解答题:
18解:(1).files/image154.gif)
.files/image156.gif)
(2)由题设,.files/image158.gif)
.files/image160.gif)
19解:(1)记“第一次与第二次取到的球上的号码的和是
.files/image162.gif)
所以第一次与第二次取到的地球上的号码的和是4的概率.files/image164.gif)
(2)记“第一次与第二次取到的上的号码的积不小于
.files/image166.gif)
|