
题目列表(包括答案和解析)
(06年湖北卷文)(12分)
设函数f(x)=x3+ax2+bx+c在x=1处取得极值-2,试用c表示a和b,并求f(x)的单调区间。
(06年湖北卷理)已知平面区域D由以![]() 为顶点的三角形内部以及边界组成。若在区域D上有无穷多个点
为顶点的三角形内部以及边界组成。若在区域D上有无穷多个点![]() 可使目标函数z=x+my取得最小值,则
可使目标函数z=x+my取得最小值,则![]() ( )
( )
A.-2 B.-1 C.1 D.4
(08年正定中学一模文)(12分)
已知函数f(x)=x3+ax2+bx+c在x=-![]() 与x=1时都取得极值
与x=1时都取得极值
(1) 求a、b的值与函数f(x)的单调区间
(2) 若对xÎ〔-1,2〕,不等式f(x)<c2恒成立,求c的取值范围。
(06年江西卷理)(12分)
已知函数f(x)=x3+ax2+bx+c在x=-![]() 与x=1时都取得极值
与x=1时都取得极值
(1)求a、b的值与函数f(x)的单调区间
(2)若对xÎ〔-1,2〕,不等式f(x)<c2恒成立,求c的取值范围。
(本题满分12分)在锐角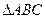 中,已知内角A、B、C所对的边分别为a、b、
中,已知内角A、B、C所对的边分别为a、b、
c,且满足2sinB(2cos2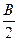 -1)=-
-1)=-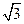 cos2B。
cos2B。
(1)求B的大小;
(2)如果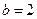 ,求
,求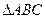 的面积
的面积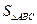 的最大值.
的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com