练习册

  • 练习册
  • 试题
    (用b表示.且). 【查看更多】

     

    题目列表(包括答案和解析)

    设函数，且在点（）处的切线垂直y轴。

       （1）用a分别表示b和c；

       （2）当bc取最小值时，求函数的单调区间。

    查看答案和解析>>

    设函数，且在点（）处的切线垂直y轴。

       （1）用a分别表示b和c；

       （2）当bc取最小值时，求函数的单调区间。

    查看答案和解析>>

    已知向量，且与之间有关系式：其中。

    （1）试用表示；

    （2）求的最小值，并求此时a与b的夹角的值。

    查看答案和解析>>

    设F（1，0），点M在x轴上，点P在y轴上，且

    （1）当点P在y轴上运动时，求点N的轨迹C的方程；

    （2）设是曲线C上的点，且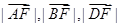成等差数列，当AD的垂直平分线与x轴交于点E（3，0）时，求点B的坐标。

    【解析】本试题主要是对于圆锥曲线的综合考查。首先求解轨迹方程，利用向量作为工具表示向量的坐标，进而达到关系式的求解。第二问中利用数列的知识和直线方程求解点的坐标。

     

    查看答案和解析>>

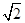    设椭圆E: （a,b>0）过M（2，） ，N(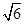,1)两点，O为坐标原点，

    （1）求椭圆E的方程；

    （2）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且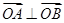？若存在，写出该圆的方程，若不存在说明理由。

    【解析】本试题主要是考查了椭圆方程的求解，待定系数法求解，并且考查了圆与椭圆的位置关系的研究，利用恒有交点，联立方程组和韦达定理一起表示向量OA,OB，并证明垂直。

     

    查看答案和解析>>

    一、ADBCC  CCBBA  DC

    二、13. ,;14. ；15. ．16.

    三、

    17.

    解: (Ⅰ)由, 是三角形内角，得……………..

    ∴ ………………………………………..

      …………………………………………………………6分

    (Ⅱ) 在中,由正弦定理， ，

    …, ,

    由余弦定理得:

                    =………………………………12分

    18.

    解：（I）已知，

           只须后四位数字中出现2个0和2个1.

                                                 …………4分

       （II）的取值可以是1，2，3，4，5，.

          

                                                                  …………8分

           的分布列是

       

    1

    2

    3

    4

    5

    P

                                                                                                          …………10分

                     …………12分

       （另解：记

           .）

    19.

    证明： 解法一：（1）取PC中点M，连结ME、MF，则MF∥CD，MF=CD，又AE∥CD，AE=CD，∴AE∥MF，且AE=MF，∴四边形AFME是平行四边形，∴AF∥EM，∵AF平面PCE，∴AF∥平面PCE. …………………………………(4分)

             (2)∵PA⊥平面ABCD，CD⊥AD. ∴CD⊥PD，∴∠PDA是二面角P-CD-B的平面角，即∠PDA=45°，   ………………………………………………………………(6分)

    ∴△PAD是等腰直角三角形，∴AF⊥PD，又AF⊥CD，∴AF⊥平面PCD，而EM∥AF，∴EM⊥平面PCD. 又EM平面PEC，∴面PEC⊥面PCD. 在平面PCD内过F作FH⊥PC于H，则FH就是点F到平面PCE的距离. …………………………………(10分)

    由已知，PD=，PF=，PC=，△PFH∽△PCD，∴，

    ∴FH=.           ………………………………………………………………(12分)

           解法二：（1）取PC中点M，连结EM，

    =+=，∴AF∥EM，又EM平面PEC，AF平面PEC，∴AF∥平面PEC. ………………………………………(4分)

    （2）以Ａ为坐标原点，分别以所在直线为x、y、z

    轴建立坐标系.　∵PA⊥平面ABCD，CD⊥AD，∴CD⊥PD，

    ∴∠PDA是二面角P-CD-B的平面角，即∠PDA=45°. ……(6分)

    ∴A(0, 0, 0), P(0, 0, 2), D(0, 2, 0), F(0, 1, 1), E, C(3, 2, 0)，

    设平面PCE的法向量为=(x, y, z)，则⊥，⊥，而=（-，0，2），

    =（，2，0），∴-x+2z=0，且x+2y=0，解得y=-x，z=x. 取x=4

    得=(4, -3, 3)，………………………………………………………………(10分)

    又=（0，1，-1），

    故点F到平面PCE的距离为d=.…………(12分)

     

    20.

     解:1)函数.又,故为第一象限角,且.

       函数图像的一条对称轴方程式是: 得又c为半点焦距，

       由知椭圆C的方程可化为

                                 （1）

       又焦点F的坐标为（），AB所在的直线方程为

                                   （2）                     （2分)

      （2）代入（1）展开整理得

                          （3）

       设A（），B（），弦AB的中点N（），则是方程（3）的两个不等的实数根，由韦达定理得

                           （4）

          

            

             即为所求。                    （5分）

    2）与是平面内的两个不共线的向量，由平面向量基本定理，对于这一平面内的向量，有且只有一对实数使得等式成立。设由1）中各点的坐标可得：

    又点在椭圆上，代入（1）式得

         

    化为：        （5）

       由（2）和（4）式得

       又两点在椭圆上，故1有入（5）式化简得：

                   

    由得到又是唯一确定的实数，且，故存在角，使成立，则有

    若，则存在角使等式成立；若由与于是用代换，同样证得存在角使等式：成立.

    综合上述，对于任意一点，总存在角使等式：成立.

                                                                         （12分）

    21．解：(Ⅰ)  

    所以函数在上是单调减函数. …………………………4分

     (Ⅱ) 证明:据题意且x1<x2<x3,

    由(Ⅰ)知f (x1)>f (x2)>f (x3),  x2=…………………………6分

    …………………8分

    即ㄓ是钝角三角形……………………………………..9分

    (Ⅲ) 假设ㄓ为等腰三角形，则只能是

     

     

     

    即

      ①          …………………………………………

    而事实上,    ②

    由于,故(2)式等号不成立.这与式矛盾. 所以ㄓ不可能为等腰三角形..13分

     

    22．

    解：⑴∵，又，为递增数列即为，

    当时，恒成立，当时，的最大值为。∴ 。∴b的取值范围是：                   （6分）

    ⑵     ①又       ②

    ①-②：

    ，

    当时，有成立，

    得与同号，于是由递推关系得与同号，因此只要就可推导。又

    ，又    ，

    即首项的取值范围是

                                                                          （13分）

     


    同步练习册答案