练习册

  • 练习册
  • 试题
    11．已知等差数列的前n项和为Sn.且S2=10.S5=55.则过点P(n,an)和Q(n+2,an+2)()的直线的一个方向向量的坐标是 【查看更多】

     

    题目列表(包括答案和解析)

    已知等差数列的前n项和为Sn，且Sp=Sq（p≠q，p、q∈N），则Sp+q=
     
    ．

    查看答案和解析>>

    已知等差数列的前n项和为Sn，且S2＝10，S5＝55，则过点P(n， )、Q(n＋2， )(n∈N+)的直线的一个方向向量的坐标为(     )

    （A）(1，1)      （B）(1，2)      （C）  (1，3)     （D）(1，4)

    查看答案和解析>>

    已知等差数列{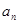}的前n项和为Sn，且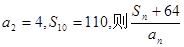的最小值为      .

     

    查看答案和解析>>

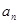    已知等差数列{}的前n项和为Sn，且S3 =6，则5a1+a7，的值为

        A．12             B．10             C．24             D．6

     

    查看答案和解析>>

    .已知等差数列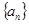的前n项和为Sn，且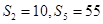则过点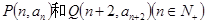的直线的斜率是______________

     

    查看答案和解析>>

     

    一、选择题

    1―12  CBDBA  ACCAD  BA

    二、填空题

    13．    14．   15．（理）   （文）16．②④

    三、解答题

    17．解（1）设向量的夹角

    则

    …………………………………………2分

    当

    向量的夹角为；…………………………4分

    当

    向量的夹角为；……………………6分

    （2）|对任意的恒成立，

    即,

    对任意的恒成立。

    即恒成立……………………8分

    所以…………………………10分

    解得：

    故所求实数的取值范围是………………12分

    18．（理）解：（1）的取值为1，3。

    又…………………………1分

    …………………………3分

    的分布列为

    1

    3

    P

     

    …………………………5分

    ………………………………6分

    （2）当S8=2时，即前8分钟出现“红灯”5次和“绿灯”3次，有已知 若第一、三分钟出现“红灯”，则其余六分钟可出现“红灯”3次………………8分

    若第一、二分钟出现“红灯”，第三分钟出现“绿灯”，则其后五分钟可出现“红灯”3次…………………………10分

    故此时的概率为……………………12分

    （文）解：（1）若第一个路口为红灯，则第二个路口为绿灯的概率为

    ；…………………………2分

    若第一个路口为绿灯，则第二个路口为绿灯的概率为…………4分

    ∴经过第二个路口时，遇到绿灯的概率是…………6分

    （2）若第一个路口为红灯，其它两个路口为绿灯的概率为

    ；…………………………8分

    若第二个路口为红灯，其它两个路口为绿灯的概率为：

    ………………………………10分

    若第三个路口为红灯，其它两个路口为绿灯的概率为：

    …………………………11分

    ∴经过三个路口，出现一次红灯，两次绿灯的概率是………………12分

    19．（理）解：（1）求满足条件①的a的取值范围，

    函数的定义域为取任意实数时，

    即…………………………2分

    解得：a<1…………………………3分

    求满足条件②的a的取值范围

    设……………………4分

    由可得，

    说明：当

    又当

    ∴对任意的实数x，恒有…………………………6分

    要使得x取任意实数时，不等式恒成立，

    须且只须…………………………7分

    由①②可得，同时满足条件（i）、（ii）的实数a的取值范围为：

    …………………………8分

    （2）

    ……………………10分

    即

    ∴不等式的解集是：

    …………………………12分

    （文）解：（1）…………4分

    （2）解法一  ………………6分

    因为，所以……………………00分

    解得：………………12分

    解法二：当x=0时，恒成立；………………5分

    当x>0时，原式或化为，………………9分

    因为时取等号）………………11分

    20．解法一：（1）连结AC，交BD于0，

    则O为AC的中点，连结EO。

    ∵PA//平面BDE，平面PAC平面BDE=OE，

    ∴PA//OE…………………………2分

    ∴点E是PC的中点。…………………………3分

    （2）∵PD⊥底面ABCD，且DC底面ABCD，

    ∴PD⊥DC，△PDC是等腰直角三角形，……………………4分

    而DE是斜边PC的中线，

    ∴DE⊥PC，  ①

    又由PD⊥平面ABCD得，PD⊥BC。…………………………6分

    ∵底面ABCD是正方形，CD⊥BC，

    ∴BC⊥平面PDC，

    而DE平面PDC，

    ∴BC⊥DE   ② ……………………7分

    由①和②推得DE⊥平面PBC，而PB平面PBC

    ∴DE⊥PB，又DF⊥PB且DEDF=D，

    所以PB⊥平面EFD，…………………………8分

    （3）由（2）知，PB⊥EF，已知PB⊥DF，故∠EFD是二面角C―PB―D的平面角，

    ………………9分

    由（2）知，DF⊥EF，PD⊥DB。

    设正方形ABCD的边长为a，则PD=DC=a，BD=

    ……………………10分

    在Rt△EFD中，

    所以，二面角C―PB―D的大小为……………………12分

     

    解法二：（1）同解法一……………………3分

    （2）如图所示建立空间直角坐标系，D为坐标原点，

    设DC=a，依题意得

    P（0，0，a），B（a,a,0），C（0，a，0   ），

    E（0， ），A（a，0，0），D（0，0，0），

    ………………4分

    …………………………6分

    由已知DF⊥PB，且DFDE=D，

    所以PB⊥平面EFD。………………………………8分

    （3）由（2）得

    设平面PBC的法向量为n=（x，y，z），

    m为平面PBD的法向量，由

    及得

    平面PBD

    又因为二面角C―PB―D为锐角，所以其大小为……………………12分

    21．解：设

    因为两准线与x轴的交点分别为

     ……………………1分

    由题意知

    ………………………………3分

    则点N的坐标为N（），

    即N………………………………4分

    所以………………5分

    则………………………………6分

           当x≠0时，代入，=得：=……………………8分

           所以，

           即                                                               …………………10分

           当x=0时，点P的坐标为P（0，），

           点M的坐标满足条件：=

           点M的坐标满足条件：=

           显然推出与已知双曲线中≠0矛盾。

           所以P点的轨迹方程为.（x≠0，y≠0）      ……………………12分

    22．解：

       （1）由………2分

           所以，

    即所求数列{an}的通项公式为………………4分

       （2）若n为奇数，则…………5分

           =……………………7分

           =4-3                                                                             …………………9分

           若n为偶数，则………………10分

           =            …………………12分

           =4-4                                                                               …………………14分

     

     


    同步练习册答案