
题目列表(包括答案和解析)
(1)当p=q=![]() 时,记ξ=|S3|,求ξ的分布列和数学期望;
时,记ξ=|S3|,求ξ的分布列和数学期望;
(2)当p=![]() ,q=
,q=![]() 时,求S8=2且Si≥0(i=1,2,3,4)的概率.
时,求S8=2且Si≥0(i=1,2,3,4)的概率.
(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
(理)某种型号汽车四个轮胎半径相同,均为 ,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为
,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为 (假定四个轮胎中心构成一个矩形). 当该型号汽车开上一段上坡路
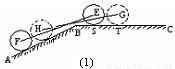
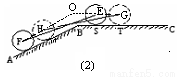
(假定四个轮胎中心构成一个矩形). 当该型号汽车开上一段上坡路 (如图(1)所示,其中
(如图(1)所示,其中 (
(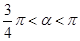 )),且前轮
)),且前轮 已在
已在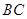 段上时,后轮中心在
段上时,后轮中心在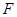 位置;若前轮中心到达
位置;若前轮中心到达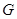 处时,后轮中心在
处时,后轮中心在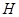 处(假定该汽车能顺利驶上该上坡路). 设前轮中心在
处(假定该汽车能顺利驶上该上坡路). 设前轮中心在 和
和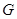 处时与地面的接触点分别为
处时与地面的接触点分别为 和
和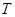 ,且
,且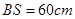 ,
,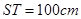 . (其它因素忽略不计)
. (其它因素忽略不计)
(1)如图(2)所示,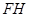 和
和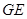 的延长线交于点
的延长线交于点 ,
,
求证: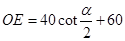 (cm);
(cm);
(2)当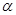 =
=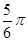 时,后轮中心从
时,后轮中心从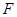 处移动到
处移动到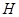 处实际移动了多少厘米? (精确到1cm)
处实际移动了多少厘米? (精确到1cm)
(09年海淀区期末理)(14分)
某种家用电器每台的销售利润与该电器的无故障使用时间T(单位:年)有关。若![]() ,则销售利润为0元,若
,则销售利润为0元,若![]() ,则销售利润为100元;若T>3,则销售利润为200元。设每台该种电器的无故障使用时间
,则销售利润为100元;若T>3,则销售利润为200元。设每台该种电器的无故障使用时间![]() ,
,![]() 及T>3这三种情况发生的概率分别为P1、P2、P3,又知P1、P2是方程
及T>3这三种情况发生的概率分别为P1、P2、P3,又知P1、P2是方程![]() 的两个根,且P2=P3。
的两个根,且P2=P3。
(I)求P1、P2、P3的值;
(II)记![]() 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求![]() 的分布列;
的分布列;
(III)求销售两台这种家用电器的销售利润总和的平均值。
(08年长沙一中一模理)某种游戏中,黑、黄两个“电子狗”从棱长为1的正方体![]() 的顶点A出发沿棱向前爬行,每爬完一条棱称为“爬完一段”。黑“电子狗”爬行的路线是
的顶点A出发沿棱向前爬行,每爬完一条棱称为“爬完一段”。黑“电子狗”爬行的路线是![]() ,黄“电子狗”爬行的路线是
,黄“电子狗”爬行的路线是![]() 它们都遵循如下规则:所爬行的第
它们都遵循如下规则:所爬行的第![]() 段与第
段与第![]() 段所在直线必须是异面直线(其中
段所在直线必须是异面直线(其中![]() 是正整数).设黑“电子狗”爬完2008段、黄“电子狗”爬完2007段后知自停止在正方体的某个顶点处,这时黑、黄“电了狗”间的距离是( )
是正整数).设黑“电子狗”爬完2008段、黄“电子狗”爬完2007段后知自停止在正方体的某个顶点处,这时黑、黄“电了狗”间的距离是( )
A.0 B.1 C.![]() D.
D.![]()
(08年黄冈市模拟理)(12分)某种彩票在一年内中奖号码的首位数字(如023的0)构成一个分布,数字0,1,2,…,9出现的概率满足![]() =f(x)=a
=f(x)=a![]() (a为常数),现在从这些中奖号码中任取一个,记其首位数字为
(a为常数),现在从这些中奖号码中任取一个,记其首位数字为![]() .
.
(1)求![]() 的分布列;
的分布列;
(2)求![]() 的期望
的期望![]() .
.
一、选择题
1―12 CBDBA ACCAD BA
二、填空题
13.%20文理科数学.files/image162.gif) 14.
14.%20文理科数学.files/image164.gif) 15.(理)
15.(理)%20文理科数学.files/image166.gif) (文)
(文)%20文理科数学.files/image168.gif) 16.②④
16.②④
三、解答题
17.解(1)设向量%20文理科数学.files/image170.gif) 的夹角
的夹角%20文理科数学.files/image172.gif)
则%20文理科数学.files/image174.gif)
%20文理科数学.files/image176.gif) …………………………………………2分
…………………………………………2分
当%20文理科数学.files/image178.gif)
向量%20文理科数学.files/image170.gif) 的夹角为
的夹角为%20文理科数学.files/image181.gif) ;…………………………4分
;…………………………4分
当%20文理科数学.files/image183.gif)
向量%20文理科数学.files/image170.gif) 的夹角为
的夹角为%20文理科数学.files/image185.gif) ;……………………6分
;……………………6分
(2)|%20文理科数学.files/image187.gif) 对任意的
对任意的%20文理科数学.files/image114.gif) 恒成立,
恒成立,
即%20文理科数学.files/image190.gif) ,
,
对任意的%20文理科数学.files/image114.gif) 恒成立。
恒成立。
即%20文理科数学.files/image193.gif) 恒成立……………………8分
恒成立……………………8分
所以%20文理科数学.files/image195.gif) …………………………10分
…………………………10分
解得:%20文理科数学.files/image197.gif)
故所求实数%20文理科数学.files/image116.gif) 的取值范围是
的取值范围是%20文理科数学.files/image200.gif) ………………12分
………………12分
18.(理)解:(1)%20文理科数学.files/image202.gif) 的取值为1,3。
的取值为1,3。
又%20文理科数学.files/image120.gif) …………………………1分
…………………………1分
%20文理科数学.files/image205.gif)
%20文理科数学.files/image207.gif) …………………………3分
…………………………3分
%20文理科数学.files/image209.gif) 的分布列为
的分布列为
%20文理科数学.files/image124.gif)
1
3
P
%20文理科数学.files/image212.gif)
%20文理科数学.files/image214.gif)
…………………………5分
%20文理科数学.files/image216.gif) ………………………………6分
………………………………6分
(2)当S8=2时,即前8分钟出现“红灯”5次和“绿灯”3次,有已知%20文理科数学.files/image218.gif) 若第一、三分钟出现“红灯”,则其余六分钟可出现“红灯”3次………………8分
若第一、三分钟出现“红灯”,则其余六分钟可出现“红灯”3次………………8分
若第一、二分钟出现“红灯”,第三分钟出现“绿灯”,则其后五分钟可出现“红灯”3次…………………………10分
故此时的概率为%20文理科数学.files/image220.gif) ……………………12分
……………………12分
(文)解:(1)若第一个路口为红灯,则第二个路口为绿灯的概率为
%20文理科数学.files/image222.gif) ;…………………………2分
;…………………………2分
若第一个路口为绿灯,则第二个路口为绿灯的概率为%20文理科数学.files/image224.gif) …………4分
…………4分
∴经过第二个路口时,遇到绿灯的概率是%20文理科数学.files/image226.gif) …………6分
…………6分
(2)若第一个路口为红灯,其它两个路口为绿灯的概率为
%20文理科数学.files/image228.gif) ;…………………………8分
;…………………………8分
若第二个路口为红灯,其它两个路口为绿灯的概率为:
%20文理科数学.files/image230.gif) ………………………………10分
………………………………10分
若第三个路口为红灯,其它两个路口为绿灯的概率为:
%20文理科数学.files/image232.gif) …………………………11分
…………………………11分
∴经过三个路口,出现一次红灯,两次绿灯的概率是%20文理科数学.files/image234.gif) ………………12分
………………12分
19.(理)解:(1)求满足条件①的a的取值范围,
函数%20文理科数学.files/image236.gif) 的定义域为
的定义域为%20文理科数学.files/image238.gif) 取任意实数时,
取任意实数时,
%20文理科数学.files/image240.gif)
即%20文理科数学.files/image242.gif) …………………………2分
…………………………2分
解得:a<1…………………………3分
求满足条件②的a的取值范围
设%20文理科数学.files/image244.gif) ……………………4分
……………………4分
由%20文理科数学.files/image246.gif) 可得,
可得,
%20文理科数学.files/image248.gif)
说明:当%20文理科数学.files/image250.gif)
又当%20文理科数学.files/image252.gif)
∴对任意的实数x,恒有%20文理科数学.files/image254.gif) …………………………6分
…………………………6分
要使得x取任意实数时,不等式%20文理科数学.files/image141.gif) 恒成立,
恒成立,
须且只须%20文理科数学.files/image257.gif) …………………………7分
…………………………7分
由①②可得,同时满足条件(i)、(ii)的实数a的取值范围为:
%20文理科数学.files/image259.gif) …………………………8分
…………………………8分
(2)%20文理科数学.files/image261.gif)
%20文理科数学.files/image263.gif)
%20文理科数学.files/image265.gif) ……………………10分
……………………10分
%20文理科数学.files/image267.gif)
即%20文理科数学.files/image269.gif)
∴不等式%20文理科数学.files/image271.gif) 的解集是:
的解集是:
%20文理科数学.files/image273.gif) …………………………12分
…………………………12分
(文)解:(1)%20文理科数学.files/image275.gif) …………4分
…………4分
(2)解法一 %20文理科数学.files/image277.gif) ………………6分
………………6分
因为%20文理科数学.files/image279.gif) ,所以
,所以%20文理科数学.files/image281.gif) ……………………00分
……………………00分
解得:%20文理科数学.files/image283.gif) ………………12分
………………12分
解法二:当x=0时,%20文理科数学.files/image285.gif) 恒成立;………………5分
恒成立;………………5分
当x>0时,原式或化为%20文理科数学.files/image287.gif) ,………………9分
,………………9分
因为%20文理科数学.files/image289.gif) 时取等号)………………11分
时取等号)………………11分
|