
题目列表(包括答案和解析)
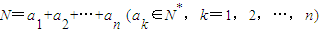 ,则称a1×a2×…×an为N的一个“分解积”.
,则称a1×a2×…×an为N的一个“分解积”.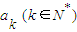 中2的个数不超过2;
中2的个数不超过2;已知 ,函数
,函数
(1)当 时,求函数
时,求函数 在点(1,
在点(1, )的切线方程;
)的切线方程;
(2)求函数 在[-1,1]的极值;
在[-1,1]的极值;
(3)若在 上至少存在一个实数x0,使
上至少存在一个实数x0,使 >g(xo)成立,求正实数
>g(xo)成立,求正实数 的取值范围。
的取值范围。
【解析】本试题中导数在研究函数中的运用。(1)中 ,那么当
,那么当 时,
时, 又
又  所以函数
所以函数 在点(1,
在点(1, )的切线方程为
)的切线方程为 ;(2)中令
;(2)中令 有
有 

对a分类讨论 ,和
,和 得到极值。(3)中,设
得到极值。(3)中,设 ,
, ,依题意,只需
,依题意,只需 那么可以解得。
那么可以解得。
解:(Ⅰ)∵ ∴
∴ 
∴ 当 时,
时, 又
又 
∴ 函数 在点(1,
在点(1, )的切线方程为
)的切线方程为 --------4分
--------4分
(Ⅱ)令 有
有 

①
当 即
即 时
时
|
|
(-1,0) |
0 |
(0, |
|
( |
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
极大值 |
|
极小值 |
|
故 的极大值是
的极大值是 ,极小值是
,极小值是
②
当 即
即 时,
时, 在(-1,0)上递增,在(0,1)上递减,则
在(-1,0)上递增,在(0,1)上递减,则 的极大值为
的极大值为 ,无极小值。
,无极小值。
综上所述  时,极大值为
时,极大值为 ,无极小值
,无极小值
 时 极大值是
时 极大值是 ,极小值是
,极小值是 ----------8分
----------8分
(Ⅲ)设 ,
,
对 求导,得
求导,得
∵ ,
,

∴  在区间
在区间 上为增函数,则
上为增函数,则
依题意,只需 ,即
,即
解得  或
或 (舍去)
(舍去)
则正实数 的取值范围是(
的取值范围是(
 ,
, )
)
16.(2)解(1)当a=1,b=-2时,g(x)=f(x)-2,把f(x)图象向下平移两个单位就可得到g(x)图象,
这时函数g(x)只有两个零点,所以(1)不对
(2)若a=-1,-2<b<0,则把函数f(x)作关于x轴对称图象,然后向下平移不超过2个单位就可得到g(x)图象,这时g(x)有超过2的零点
(3)当a<0时, y=af(x)根据定义可断定是奇函数,如果b≠0,把奇函数y=af(x)图象再向上(或向下)平移后才是y=g(x)=af(x)+b的图象,那么肯定不会再关于原点对称了,肯定不是奇函数;当b=0时才是奇函数,所以(3)不对。所以正确的只有(2)
为了考察高中生学习语文与数学之间的关系,在某中学学生中随机地抽取了610名学生得到如下列表:
|
数学 | 及格 | 不及格 | 总计 |
| 及格 | 310 | 142 | 452 |
| 不及格 | 94 | 64 | 158 |
| 总计 | 404 | 206 | 610 |
由表中数据计算及![]() 的观测值
的观测值![]() 问在多大程度上可以认为高中生的语文与数学成绩之间有关系?为什么?
问在多大程度上可以认为高中生的语文与数学成绩之间有关系?为什么?
16.(2)解(1)当a=1,b=-2时,g(x)=f(x)-2,把f(x)图象向下平移两个单位就可得到g(x)图象,
这时函数g(x)只有两个零点,所以(1)不对
(2)若a=-1,-2<b<0,则把函数f(x)作关于x轴对称图象,然后向下平移不超过2个单位就可得到g(x)图象,这时g(x)有超过2的零点
(3)当a<0时, y=af(x)根据定义可断定是奇函数,如果b≠0,把奇函数y=af(x)图象再向上(或向下)平移后才是y=g(x)=af(x)+b的图象,那么肯定不会再关于原点对称了,肯定不是奇函数;当b=0时才是奇函数,所以(3)不对。所以正确的只有(2)
一盒中放有大小相同的红色、绿色、黄色三种小球,已知红球个数是绿球个数的两倍,黄球个数是绿球个数的一半,现在从该盒中随机取出一球,若取出红球得1分,取出黄球得0分,取出绿球得-1分,试写出从该盒中取出一球所得分数Y的分布列.
 语文 语文数学 | 及格 | 不及格 | 总计 |
| 及格 | 310 | 142 | 452 |
| 不及格 | 94 | 64 | 158 |
| 总计 | 404 | 206 | 610 |
 的观测值
的观测值 问在多大程度上可以认为高中生的语文与数学成绩之间有关系?为什么?
问在多大程度上可以认为高中生的语文与数学成绩之间有关系?为什么?1. 构造向量 ,
, ,所以
,所以 ,
, .由数量积的性质
.由数量积的性质 ,得
,得 ,即
,即 的最大值为2.
的最大值为2.
2. ∵ ,令
,令 得
得 ,所以
,所以 ,当
,当 时,
时, ,当
,当 时,
时, ,所以当
,所以当 时,
时, .
.
3.∵ ,∴
,∴ ,
, ,又
,又 ,∴
,∴ ,则
,则 ,所以周期
,所以周期 .作出
.作出 在
在 上的图象知:若
上的图象知:若 ,满足条件的
,满足条件的 (
( )存在,且
)存在,且 ,
, 关于直线
关于直线 对称,
对称, ,
, 关于直线
关于直线 对称,∴
对称,∴ ;若
;若 ,满足条件的
,满足条件的 (
( )存在,且
)存在,且 ,
, 关于直线
关于直线 对称,
对称, ,
, 关于直线
关于直线 对称,
对称,
 ∴
∴ .
.
4. 不等式 (
( )表示的区域是如图所示的菱形的内部,
)表示的区域是如图所示的菱形的内部,
∵
 ,
,
当 ,点
,点 到点
到点 的距离最大,此时
的距离最大,此时 的最大值为
的最大值为 ;
;
当 ,点
,点 到点
到点 的距离最大,此时
的距离最大,此时 的最大值为3.
的最大值为3.
5. 由于已有两人分别抽到5和14两张卡片,则另外两人只需从剩下的18张卡片中抽取,共有 种情况.抽到5 和14的两人在同一组,有两种情况:
种情况.抽到5 和14的两人在同一组,有两种情况:
(1) 5 和14 为较小两数,则另两人需从15~20这6张中各抽1张,有 种情况;
种情况;
(2) 5 和14 为较大两数,则另两人需从1~4这4张中各抽1张,有 种情况.
种情况.
于是,抽到5 和14 两张卡片的两人在同一组的概率为 .
.
 6. ∵
6. ∵ ,∴
,∴ ,
,
设 ,
, ,则
,则 .
.
作出该不等式组表示的平面区域(图中的阴影部分 ).
).
令 ,则
,则 ,它表示斜率为
,它表示斜率为 的一组平行直线,易知,当它经过点
的一组平行直线,易知,当它经过点 时,
时, 取得最小值.
取得最小值.
解方程组 ,得
,得 ,∴
,∴
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com