【解析图片】设二次函数f（x）=ax²+bx+c（a，b，c∈R）满足f（-1）=0，且对任意实数x，均有x-1≤f（x）≤x²-3x+3恒成立．
（1）求f（x）的表达式；
（2）若关于x的不等式f（x）≤nx-1的解集非空，求实数n的取值的集合A．
（3）若关于x的方程f（x）=nx-1的两根为x₁，x₂，试问：是否存在实数m，使得不等式m²+tm+1≤|x₁-x₂|对任意n∈A及t∈[-3，3]恒成立？若存在，求出m的取值范围；若不存在，说明理由．

若某产品的直径长与标准值的差的绝对值不超过1mm 时，则视为合格品，否则视为不合格品。在近期一次产品抽样检查中，从某厂生产的此种产品中，随机抽取5000件进行检测，结果发现有50件不合格品。计算这50件不合格品的直径长与标准值的差（单位：mm）, 将所得数据分组，得到如下频率分布表：

分组	频数	频率
[-3, -2)		0.10
[-2, -1)	8
（1,2]		0.50
（2,3]	10
（3,4]
合计	50	1．00

（Ⅰ）将上面表格中缺少的数据填在答题卡的相应位置；

（Ⅱ）估计该厂生产的此种产品中，不合格品的直径长与标准值的差落在区间（1,3]内的概率；

（Ⅲ）现对该厂这种产品的某个批次进行检查，结果发现有20件不合格品。据此估算这批产品中的合格品的件数。

【解析】（Ⅰ）

分组	频数	频率
[-3, -2)	5	0.10
[-2, -1)	8	0.16
（1,2]	25	0.50
（2,3]	10	0.2
（3,4]	2	0.04
合计	50	1．00

（Ⅱ）根据频率分布表可知，落在区间（1,3]内频数为35，故所求概率为0.7.

（Ⅲ）由题可知不合格的概率为0.01，故可求得这批产品总共有2000，故合格的产品有1980件。

 

2011年3月日本发生的9.0级地震引发了海啸和核泄漏。核专家为检测当地动物受核辐射后对身体健康的影响，随机选取了110只羊进行检测。其中身体健康的50只中有30只受到高度辐射，余下的60只身体不健康的羊中有10只受轻微辐射。

（1）作出2×2列联表

（2）判断有多大把握认为羊受核辐射对身体健康有影响？

【解析】本试题主要考查了列联表的运用，以及判定两个分类变量之间的相关性问题的运用首先根据题意得到2×2列联表：，然后求解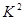的观测值为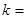

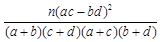
因为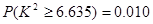，因此可知有99％的把握可以认为羊受核辐射对身体健康有影响。

解：（1）2×2列联表：

辐射程度健康类型	高度辐射	轻微辐射	合   计
身体健康	30	20	50
身体不健康	50	10	60
合  计	80	30	110

 

 

--------5分

 

-

 

（Ⅱ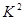）的观测值为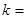

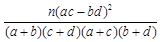
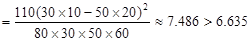     -----9分

而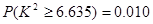 

∴有99％的把握可以认为羊受核辐射对身体健康有影响。

 

在四棱锥中，平面，底面为矩形，.

（Ⅰ）当时，求证：；

（Ⅱ）若边上有且只有一个点，使得，求此时二面角的余弦值.

【解析】第一位女利用线面垂直的判定定理和性质定理得到。当a=1时，底面ABCD为正方形，

又因为,………………2分

又，得证。

第二问，建立空间直角坐标系，则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)……4分

设BQ=m，则Q(1，m,0)(0《m《a》

要使，只要

所以，即………6分

由此可知时，存在点Q使得

当且仅当m=a-m，即m=a/2时，BC边上有且只有一个点Q，使得

由此知道a=2,  设平面POQ的法向量为

,所以    平面PAD的法向量

则的大小与二面角A-PD-Q的大小相等所以

因此二面角A-PD-Q的余弦值为

解：(Ⅰ)当时，底面ABCD为正方形，

又因为,又………………3分

(Ⅱ) 因为AB,AD,AP两两垂直，分别以它们所在直线为X轴、Y轴、Z轴建立坐标系，如图所示，

则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)…………4分

设BQ=m，则Q(1，m,0)(0《m《a》要使，只要

所以，即………6分

由此可知时，存在点Q使得

当且仅当m=a-m，即m=a/2时，BC边上有且只有一个点Q，使得由此知道a=2,

设平面POQ的法向量为

,所以    平面PAD的法向量

则的大小与二面角A-PD-Q的大小相等所以

因此二面角A-PD-Q的余弦值为

 

已知三棱锥P—ABC中，PC⊥底面ABC，,，二面角P-AB-C为，D、F分别为AC、PC的中点，DE⊥AP于E．

（Ⅰ）求证：AP⊥平面BDE；                

（Ⅱ）求直线EB与平面PAC所成的角。

【解析】本试题主要考查了线面的垂直问题以及线面角的求解的综合运用。