
题目列表(包括答案和解析)
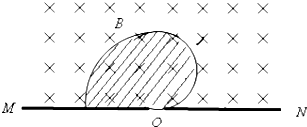
| mv2 |
| r |
| mv |
| qB |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| mv |
| Bq |
| mv |
| qB |
| 3 |
| 2 |
| mv |
| Bq |
思路解析:本题主要考查分子大小的估算.每个铜原子所占的空间应等于摩尔体积跟物质的量的比值,根据摩尔质量和密度可以求出摩尔体积.
(1)铜的相对原子量为64,即每摩尔铜质量为64 g,其摩尔体积Vmol=![]() =
=![]() m3
m3
每个铜原子的体积V0=![]() ,由以上两式得V0=1.19×10-29 m3.
,由以上两式得V0=1.19×10-29 m3.
(2)把铜原子作为球形模型,设其直径为d,则![]() π(
π(![]() )3=V0,代入数据,解得:
)3=V0,代入数据,解得:
d=2.83×10-10 m.
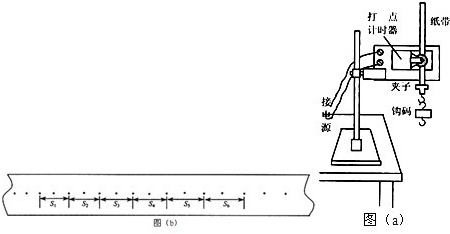
| 距离 | x1 | x3 | x5 |
| 测量值/cm |
| x5-x3 |
| 2△t |
| x5-x3 |
| 2△t |
| v4-v2 |
| 2△t |
| v4-v2 |
| 2△t |
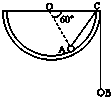 (2009?闸北区二模)如图所示,一个半径为R的半球形的碗固定在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的.一根轻质细线跨在碗口上,线的两端分别系有小球A和B,当它们处于平衡状态时,小球A与O点的连线与水平线的夹角为60°.
(2009?闸北区二模)如图所示,一个半径为R的半球形的碗固定在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的.一根轻质细线跨在碗口上,线的两端分别系有小球A和B,当它们处于平衡状态时,小球A与O点的连线与水平线的夹角为60°.| 2 |
| 2 |
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com