
题目列表(包括答案和解析)
请考生在第22、23两题中任选一题作答,如果多做,则按所做的第一题记分.
(本小题满分10分)选修4—1:几何证明选讲
如图,⊙O1与⊙O2相交于A、B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1、⊙O2于点D、E,DE与AC相交于点P.
(Ⅰ)求证:AD∥EC; (Ⅱ)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.
(Ⅱ)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.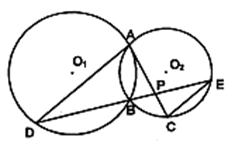
请考生在第22、23两题中任选一题作答,如果多做,则按所做的第一题记分.
(本小题满分10分)选修4—1:几何证明选讲
如图,⊙O1与⊙O2相交于A、B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1、⊙O2于点D、E,DE与AC相交于点P.
(Ⅰ)求证:AD∥EC;
 (Ⅱ)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.
(Ⅱ)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.

 (Ⅱ)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.
(Ⅱ)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.
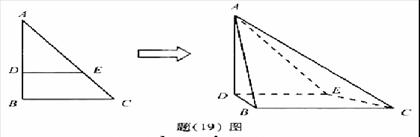
(重庆卷理19)如题(19)图,在![]() 中,B=
中,B=![]() ,AC=
,AC=![]() ,D、E两点分别在AB、AC上.使
,D、E两点分别在AB、AC上.使![]() ,DE=3.现将
,DE=3.现将![]() 沿DE折成直二角角,求:
沿DE折成直二角角,求:
(Ⅰ)异面直线AD与BC的距离;
(Ⅱ)二面角A-EC-B的大小(用反三角函数表示).
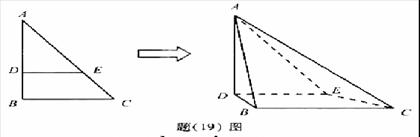
(重庆卷理19)如题(19)图,在![]() 中,B=
中,B=![]() ,AC=
,AC=![]() ,D、E两点分别在AB、AC上.使
,D、E两点分别在AB、AC上.使![]() ,DE=3.现将
,DE=3.现将![]() 沿DE折成直二角角,求:
沿DE折成直二角角,求:
(Ⅰ)异面直线AD与BC的距离;
(Ⅱ)二面角A-EC-B的大小(用反三角函数表示).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com