
题目列表(包括答案和解析)
设函数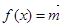 ·
·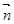 ,其中向量
,其中向量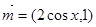 ,
,
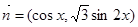 ,
,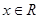 。
。
(1)求f (x)的最小正周期与单调递减区间;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,已知f (A) =2,b = 1,
△ABC的面积为 ,求△ABC 外接圆半径R的值。
,求△ABC 外接圆半径R的值。
设函数 ·
· ,其中向量
,其中向量 ,
, ,
, 。
。
(1)求f (x)的最小正周期与单调递减区间;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,已知f (A) =2,b = 1,
△ABC的面积为 ,求△ABC 外接圆半径R的值。
,求△ABC 外接圆半径R的值。
 ,其中a∈R。
,其中a∈R。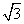 sinx),x∈R。
sinx),x∈R。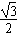 ,求
,求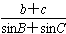 的值。
的值。 sinωxcosωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
sinωxcosωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈( ,1)。
,1)。 ,求函数f(x)的值域。
,求函数f(x)的值域。一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
答案
D
B
B
D
A
B
C
D
C
a
二 填空题:
11:f-1(x)=lnx-1 (x>0). 12:-30
13: 14:1
14:1
15:①②④;
三、解答题
16. ………………………………………………… 2分
………………………………………………… 2分
⑴当 时,
时, ,………………………………… 3分
,………………………………… 3分
则
 ,…………………………………… 5分
,…………………………………… 5分
∴
 ={x│3≤x≤5}………………………………………… 7分
={x│3≤x≤5}………………………………………… 7分
⑵∵ ,
, ,
,
∴有 ,解得
,解得 ,…………………………… 10分
,…………………………… 10分
此时 ,符合题意.………………………… 12分
,符合题意.………………………… 12分
17.解:⑴∴ =(sinα,1)共线
=(sinα,1)共线
∴sinα+cosα= ………………………………… 2分
………………………………… 2分
故sin2α=-
从而(sinα-cosα)2=1-sin2α= ……………………… 4分
……………………… 4分
∴α∈(- )∴sinα<0,cosα>0
)∴sinα<0,cosα>0
∴sinα-cosα=- ……………………………………………6分
……………………………………………6分
⑵∵ =2cos2α=1+cos2α…9分
=2cos2α=1+cos2α…9分
又cos2α=cos2α-sin2α=(cosα+sinα)(cosα-sinα)=
∴原式=1+ …………………………………………………… 12分
…………………………………………………… 12分
18.
解:⑴




 ....................................2分
....................................2分
又 也满足上式,
也满足上式,


 (
( )
)
 数列
数列 是公比为2,首项为
是公比为2,首项为 的等比数列...........4分
的等比数列...........4分

 ...........................6分
...........................6分
⑵


 .................9分
.................9分
于是 ...................12分
...................12分
19.⑴设
 …………………………2分
…………………………2分
 …………4分
…………4分
⑵由⑴,得

 …………6分
…………6分
(i)当
 …………8分
…………8分
(ii)
 …………10分
…………10分
(iii)当
 …………12分
…………12分
综上所述, ………………………………13分
………………………………13分
20.解:⑴令 ………………………… 1分
………………………… 1分
 ……………………………………… 2分
……………………………………… 2分
当-2<x≤0时 g’‘(x)≤0;当x>0时,g‘(x)>0…………………… 3分
∴g(x)在(-2,0 上递减,在(0,+∞)上递增……………………… 4分
上递减,在(0,+∞)上递增……………………… 4分
则x=0时 g(x)min=g(0)=0 g(x)≥g(x)min=0 ………………… 5分
即fn(x)≥nx ……………… 6分
⑵∵ 即
即 …………… 7分
…………… 7分
 易得x0>0 …………………………… 9分
易得x0>0 …………………………… 9分
而
由⑴知x>0时(1+x)n>1+nx 故2n+1=(1+1)n+1>n+2 ∴x0<1… 12分
综上0<x0<1 ……………………………… 13分
21.解:⑴由已知,当n=1时,a ,∵a1>0,∴a1=1. ………… 1分
,∵a1>0,∴a1=1. ………… 1分
当n≥2时, …+
…+ ①
①
 …+
…+ ②
②
由①―②得,a ……………………………………………3分
……………………………………………3分
∵an>0, ∴a =2Sn-1+an,即a
=2Sn-1+an,即a =2Sn-an,
=2Sn-an,
当n=1时,∴a1=1适合上式,
∴a ………………………………………………………5分
………………………………………………………5分
⑵由⑴知,a ,即a
,即a =2Sn-an(n∈
=2Sn-an(n∈ )③
)③
当n≥2时,a =2Sn-1-an-1
④
=2Sn-1-an-1
④
由③―④得,
a =2(Sn-Sn-1)-an+an-1=2an-an+an-1=an+an-1……………………………7分
=2(Sn-Sn-1)-an+an-1=2an-an+an-1=an+an-1……………………………7分
∵an+an-1>0,∴an-an-1=1,数列{an}是等差数列,首项为1,公差为1,
可得an=n. …………………………………………………………………9分
(3)∵an=n,∴bn=3n+(-1)n-1λ? =3n+(-1)n-1λ?2n, …………………10分
=3n+(-1)n-1λ?2n, …………………10分
要使bn+1> bn恒成立,
bn+1-bn=3n+1+(-1)nλ?2n+1-[3n+(-1)n-1λ?2n]
=2?3n-3λ(-1)n-1?2n>0恒成立
则(-1)n-1?λ<( )n-1恒成立…………………………………………11分
)n-1恒成立…………………………………………11分
当n为奇数时,即为λ<( )n-1恒成立
)n-1恒成立
又( )n-1的最小值为1, ∴λ<1
)n-1的最小值为1, ∴λ<1
当n为偶数时,即为λ>-( )n-1恒成立
)n-1恒成立
又-( )n-1最大值为-
)n-1最大值为- ∴λ>-
∴λ>- ……………………………12分
……………………………12分
∴- <λ<1,又λ≠0,∴λ=-1 ∴λ=-1,使得对任意n∈
<λ<1,又λ≠0,∴λ=-1 ∴λ=-1,使得对任意n∈ ,都有bn+1>bn……………13分
,都有bn+1>bn……………13分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com