练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

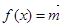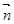    设函数·，其中向量，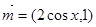

    ，。

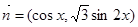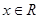    （1）求f (x)的最小正周期与单调递减区间；

    （2）在△ABC中，a、b、c分别是角A、B、C的对边，已知f (A) =2，b = 1，

    △ABC的面积为，求△ABC 外接圆半径R的值。

     

    【答案】

    （1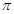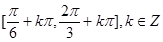），（2）R=1

    【解析】本试题主要是考查了三角函数的性质和解三角形的综合运用。

    （1）先根据向量的数量积运算表示出函数f（x），再由二倍角公式和两角和与差的公式进行化简，根据T公式可求得最小正周期，再由正弦函数的单调性可求得单调递增区间．

    （2）由f(A) = 2，得，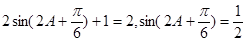

    在△ABC中，，，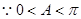

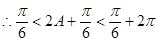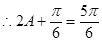    ，解得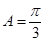，表示面积得到。

    解：（1）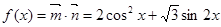

     ，

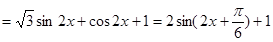    ∴函数f(x)的最小正周期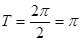。............3分

    令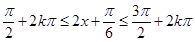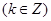，解得。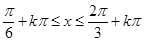

    ∴函数f(x)的单调递减区间是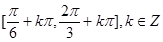。........... 6分

    （2）由f(A) = 2，得，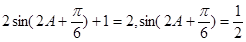

    在△ABC中，，，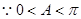

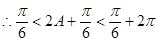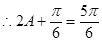    ，解得。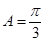

    又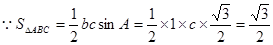，解得c = 2，

    △ABC中，由余弦定理得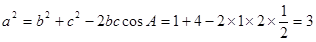：，∴a =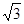

    根据正弦定理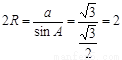，得R=1。............12分

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知向量
    a
    =(1，cos(ωx-
    π
    6
    ))    ，
    b
    =(2，2sin(ωx-
    π
    6
    ))    ，其中ω为常数，且ω＞0．
    （1）若ω=1，且
    a
    ∥
    b
    ，求tanx的值；
    （2）设函数f(x)=
    a
    •
    b
    -2    ，若f（x）的最小正周期为π，求f（x）在x∈[0，
    π
    2
    ]    时的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f（x）=
    a
    •
    b
    ，其中向量
    a
    =（2cosx，1），
    b
    =（cosx，
    		3
    sin2x）．若f（x）=1-
    		3
    ，且x∈[-
    π
    3
    ，
    π
    3
    ]，求x．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f(x)=
    a
    •
    b
    ，其中向量
    a
    =(m，cos2x)    ，
    b
    =(1+sin2x，1)    ，x∈R，且y=f（x）的图象经过点(
    π
    4
    ，2)    ．
    （Ⅰ）求实数m的值；
    （Ⅱ）求函数f（x）的最小值及此时x值的集合．
    （Ⅲ）f（x）的图象可由g（x）=1+
    		2
    sin2x如何变换得到？

    查看答案和解析>>

    科目：高中数学 来源：101网校同步练习　高三数学　苏教版(新课标·2004年初审) 苏教版 题型：044

    设f(x)，其中向量，，

    (Ⅰ)当ω＝1，时，求函数f(x)的值域；

    (Ⅱ)当ω＝－1时，求函数f(x)的单调递减区间．

    查看答案和解析>>

    科目：高中数学 来源：2010年山东省高一下学期期末考试数学卷 题型：解答题

    (本题满分12分).设函数f(x)= ·,其中向量=（,）,

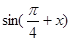
     =(,),xR求：

    （1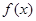）的解析式并进行化简；

    （2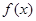）的周期和单调递增区间；

    （3）若关于的方程在上有解，求实数的取值范围。

     

    查看答案和解析>>

    同步练习册答案